Kaggle Facial Keypoints DetectionをKerasで実装する
KaggleのチュートリアルにもなっているDaniel NouriさんのUsing convolutional neural nets to detect facial keypoints tutorial という記事の流れに沿って、Facial Keypoints DetectionをKerasで実装していきます。単純なモデルから徐々に複雑にしながら解説していきます。多少の機械学習の知識があることを前提にしますが、なるべく分かりやすく解説していきたいと思います。間違い・質問・提案などあれば遠慮なく連絡してください。
KerasはPythonで書くことができるTheanoとTensorFlowベースのライブラリです。直感的に書くことができる人気急上昇中のライブラリです。2015年3月に初公開され、2016年4月にKeras 1.0が公開されました。
Danielさんの記事ではLasagneというTheanoベースのライブラリで実装しています。KerasとLasagneでデフォルトのパラメータの値が異なることなどから、元記事とは多少結果が異なる場合があります。
目次
- 事前準備
- データ
- モデル1:中間層1層
- 結果の確認
- モデル2:畳み込み
- Data Augmentation
- 学習係数の変更
- ドロップアウト
- Early Stopping
- モデルの特化
- 転移学習
- まとめ
事前準備
TheanoまたはTensorFlowをインストールしておき、
sudo pip install keras
を実行するだけで、簡単にKerasをインストールすることができます。
TheanoとTensorFlowを切り換えるのは非常に簡単で、~/.keras/keras.jsonのbackendの値をtheanoやtensorflowに書き換えるだけです。
{"epsilon": 1e-07, "floatx": "float32", "backend": "theano"}
実行時には “Using Theano backend.” のように出力されるので、バックエンドとしてどちらを使用しているかすぐに分かります。
GPUを使用して実行したい場合はAWSを利用することができます。コストを抑えることができるスポットインスタンスがおすすめです。既に必要なものがインストールされているAMIを使ってインスタンスを立ち上げればすぐに実行することができます。
例えば、スタンフォード大学が作成したami-125b2c72という公開されているAMIを利用することができます。(この中のKerasなど一部のバージョンが古くなってしまっているので、インストールし直す必要があります。)
TensorFlowは、GPUが存在する環境下では自動的にGPUを使用して実行するようになっています。一方、バックエンドがTheanoの場合は手動で指定する必要があります。実行時に
THEANO_FLAGS=device=gpu,floatX=float32 python my_keras_script.py
のようにフラグを使用する方法や、.theanorcという設定ファイルを書き換える方法があります。
データ
Facial Keypoints Detectionチャレンジの訓練データは7,049枚、96x96ピクセルのグレースケールの画像から成ります。
このチャレンジでは、left_eye_center、right_eye_outer_corner、mouth_center_bottom_lipのようなkeypoints(顔の特徴的な場所)15ヶ所(それぞれx, y座標を持つ)を学習し、推定します。
注意しなければならないのは、データが一部欠けていることです。Keypointによってはデータがたくさん存在するものもあれば、比較的データが少ないものもあります。
例えば、left_eye_center_xは7,034個のデータが存在しますが、left_eye_inner_corner_xは2,266個しか存在しません。
それでは、PythonでCSVデータを読み込んでみましょう。訓練データとテストデータを読み込む関数を書きます。この部分はKerasやLasagneを使用しないので、Danielさんのコードと同様に行います。
# -*- encoding: utf-8 -*-
# file kfkd.py
import os
import numpy as np
from pandas.io.parsers import read_csv
from sklearn.utils import shuffle
FTRAIN = 'data/training.csv'
FTEST = 'data/test.csv'
def load(test=False, cols=None):
"""testがTrueの場合はFTESTからデータを読み込み、Falseの場合はFTRAINから読み込みます。
colsにリストが渡された場合にはそのカラムに関するデータのみ返します。
"""
fname = FTEST if test else FTRAIN
df = read_csv(os.path.expanduser(fname)) # pandasのdataframeを使用
# スペースで句切られているピクセル値をnumpy arrayに変換
df['Image'] = df['Image'].apply(lambda im: np.fromstring(im, sep=' '))
if cols: # カラムに関連するデータのみを抽出
df = df[list(cols) + ['Image']]
print(df.count()) # カラム毎に値が存在する行数を出力
df = df.dropna() # データが欠けている行は捨てる
X = np.vstack(df['Image'].values) / 255. # 0から1の値に変換
X = X.astype(np.float32)
if not test: # ラベルが存在するのはFTRAINのみ
y = df[df.columns[:-1]].values
y = (y - 48) / 48 # -1から1の値に変換
X, y = shuffle(X, y, random_state=42) # データをシャッフル
y = y.astype(np.float32)
else:
y = None
return X, y
X, y = load()
print("X.shape == {}; X.min == {:.3f}; X.max == {:.3f}".format(
X.shape, X.min(), X.max()))
print("y.shape == {}; y.min == {:.3f}; y.max == {:.3f}".format(
y.shape, y.min(), y.max()))
CSVファイルからデータを読み込んだ後、Xとyの値をスケーリングしています。特徴量によって大きさがばらばらだと、学習が遅くなってしまったり、アルゴリズムによってはうまく機能しない場合があるため、このようにスケーリングや規格化を行うのが一般的です。
出力結果は以下のようになります。
left_eye_center_x 7039
left_eye_center_y 7039
right_eye_center_x 7036
right_eye_center_y 7036
left_eye_inner_corner_x 2271
left_eye_inner_corner_y 2271
left_eye_outer_corner_x 2267
left_eye_outer_corner_y 2267
right_eye_inner_corner_x 2268
right_eye_inner_corner_y 2268
right_eye_outer_corner_x 2268
right_eye_outer_corner_y 2268
left_eyebrow_inner_end_x 2270
left_eyebrow_inner_end_y 2270
left_eyebrow_outer_end_x 2225
left_eyebrow_outer_end_y 2225
right_eyebrow_inner_end_x 2270
right_eyebrow_inner_end_y 2270
right_eyebrow_outer_end_x 2236
right_eyebrow_outer_end_y 2236
nose_tip_x 7049
nose_tip_y 7049
mouth_left_corner_x 2269
mouth_left_corner_y 2269
mouth_right_corner_x 2270
mouth_right_corner_y 2270
mouth_center_top_lip_x 2275
mouth_center_top_lip_y 2275
mouth_center_bottom_lip_x 7016
mouth_center_bottom_lip_y 7016
Image 7049
dtype: int64
X.shape == (2140, 9216); X.min == 0.000; X.max == 1.000
y.shape == (2140, 30); y.min == -0.920; y.max == 0.996
Keypoint毎にいくつデータが存在するかが表示されています。y.shape == (2140, 30) というのは、keypointに関するカラムが30個あって、2140個のサンプルがあることを意味します。(15種類のkeypointがそれぞれx, y座標を持つため30個になります。)
df = df.dropna()
によって一つでもkeypointの値が存在しないサンプルは捨てられています。全てのkeypointの値が存在するサンプルは2140個しかありません。訓練データの約70%に相当するサンプルを捨ててしまうのはもったいないですが、捨てずにうまく活用する方法については記事の後半で解説します。
モデル1:中間層1層
まずは、中間層が1層の場合の普通のニューラルネットワークを実装してみます。これは単純なモデルで計算量が少ないので、CPUでもそれほど時間がかからずに終わります。
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
model = Sequential()
model.add(Dense(100, input_dim=9216))
model.add(Activation('relu'))
model.add(Dense(30))
sgd = SGD(lr='0.01', momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
hist = model.fit(X, y, nb_epoch=100, validation_split=0.2)
Kerasではこのように非常に直感的にコードを書くことができます。機械学習の知識がある人であれば、Kerasを触ったことがなくともどういうモデルなのかすぐに分かるのではないでしょうか。
96x96 = 9216の画像がインプットされます。中間層のニューロン数は100です。活性化関数はReLU (rectified linear unitの略)を使用しています。近年最もよく使われる活性化関数です。ReLUは f(x) = max(0, x)で表される関数で、下図の青線の形をしています。
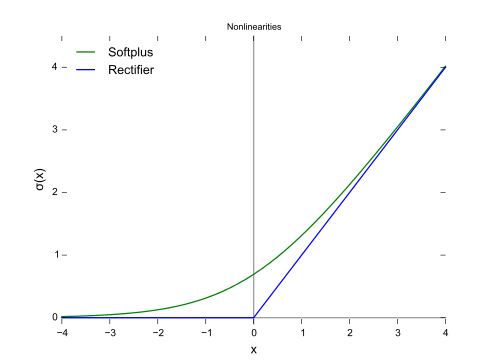
Wikipediaより引用
LasagneではReLUがデフォルトの活性化関数になっていますが、Kerasではlinear、つまりデフォルトでは活性化関数は適用されません。
オプティマイザはここではNesterov accelerated gradient (NAG)を使用しますが、他にもSGD(確率的勾配降下法)、Momentum、Adagrad、RMSprop、Adamなどがあります。SGDでは
x += - learning_rate * grad
のように勾配を直接使ってパラメータを更新します。
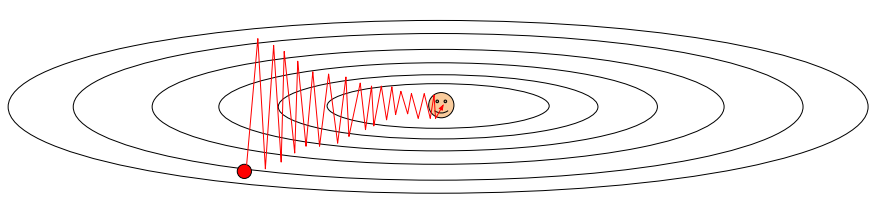
物理的な見方をすると、ポテンシャルの山(または谷)があってその斜面をボールが滑り落ちていく運動に例えることができます。SGDでは、力が加わる方向にボールを移動することに相当しますが、物理ではそのように力が直接位置を変化させるわけではありません。力が速度を変化させ、速度が位置を変えます。そのような更新の仕方に対応するのがMomentumです。
v = mu * v - learning_rate * grad
x += v
同じ方向に力を受け続けると- learning_rate * gradによってその方向にどんどん加速していきます。muはモメンタムと呼ばれるハイパーパラメータですが、物理的な描写ではむしろ空気摩擦のようなものに対応します。0.9という値がよく使われます。この摩擦によって運動エネルギーが抜かれ、最後にポテンシャルの谷の底に落ち着くことができます。
SGDでは、上図のように大きな勾配の影響を受けてターゲットに近づくのに時間がかかり過ぎてしまう問題があります。Momentumでは小さい勾配の方向の速度を徐々に大きくし、より早くターゲットに近づくことができます。
Nesterov accelerated gradient は Momentumの改良版で、位置xで勾配を求めるのではなく位置x + mu * vでの勾配を求めます。これによって坂を下り切ってまた登り始める前に少し先の勾配を検知し、減速し始めることができます。
cache += grad**2
x += - learning_rate * grad / (np.sqrt(cache) + eps)
Adagradでは勾配のキャッシュを使って規格化しています。勾配が小さいものや更新頻度が少ないものほど実質的な学習係数が大きくなり、小さな勾配をとらえることができるようになります。epsは1e-7のような非常に小さな値で、ゼロで割るのを防ぐためのものです。
Adagradの弱点は、一方的にキャッシュが溜まっていくため、学習を続けていくと実質的な学習係数が非常に小さくなってしまうことです。この改良版がRMSpropやAdamです。詳細はこちらの記事を参考にしてみてください。
よく引用されるアニメーションをここにも貼っておきたいと思います。
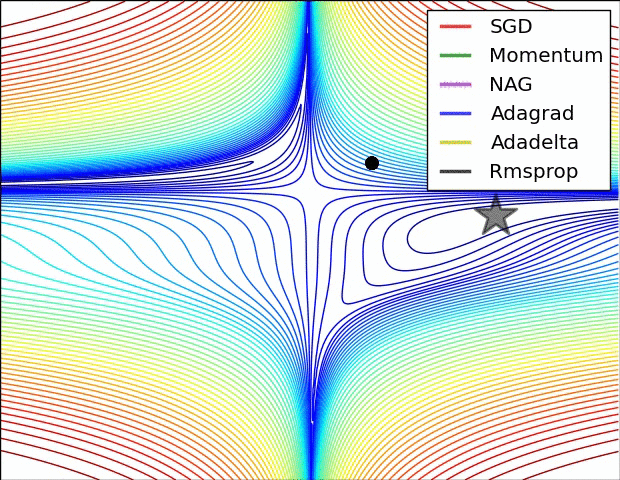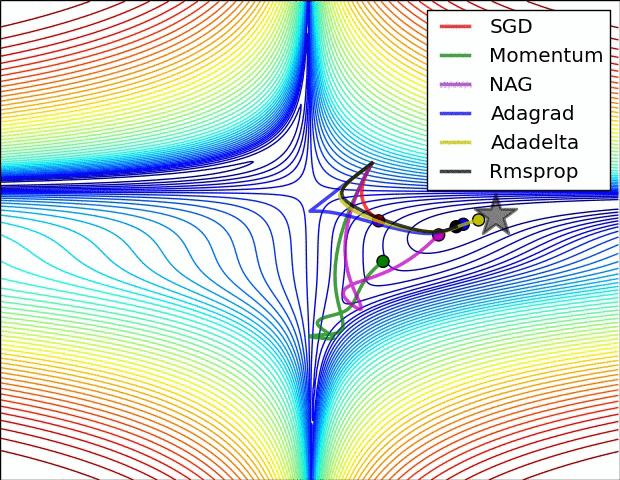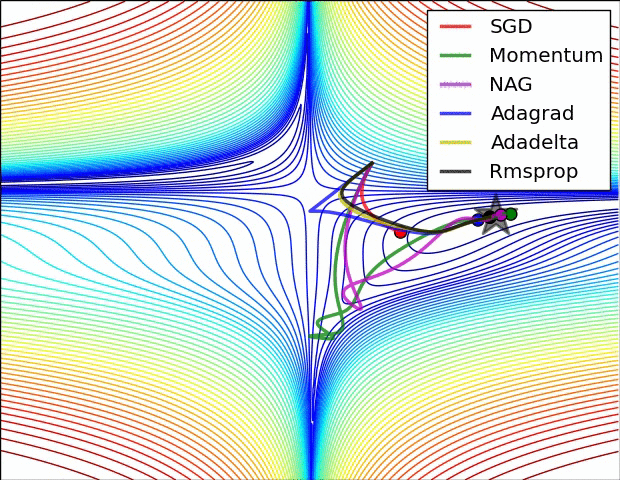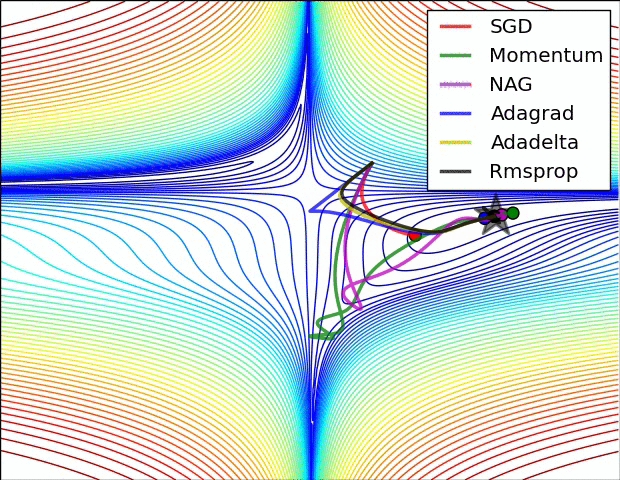
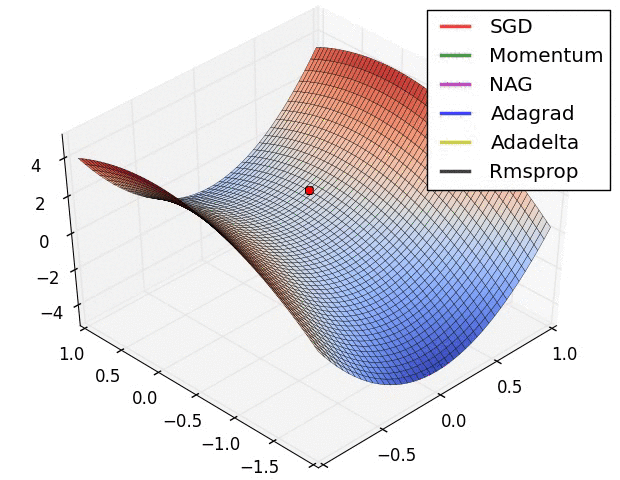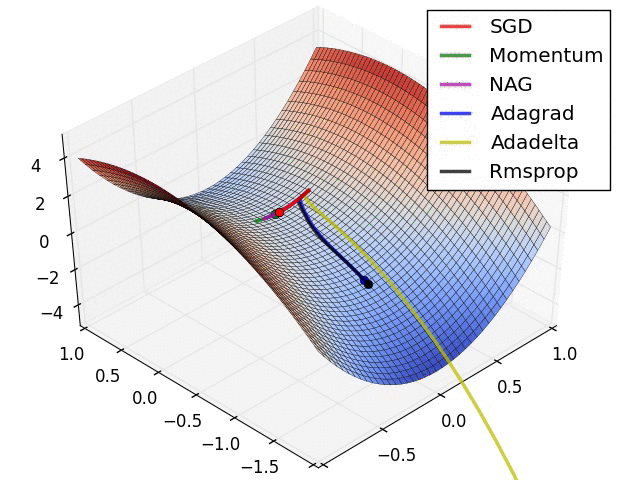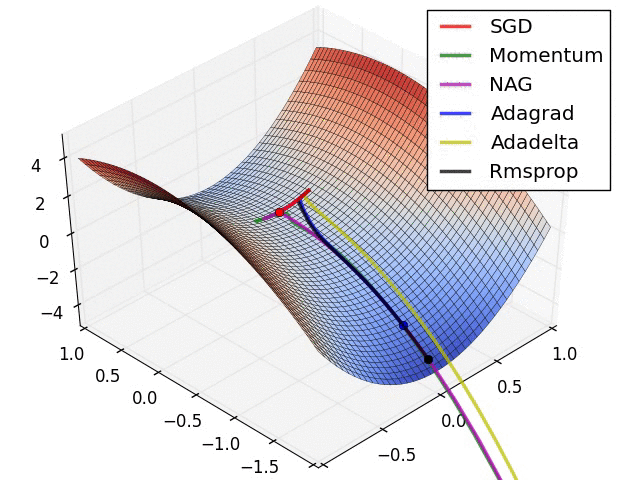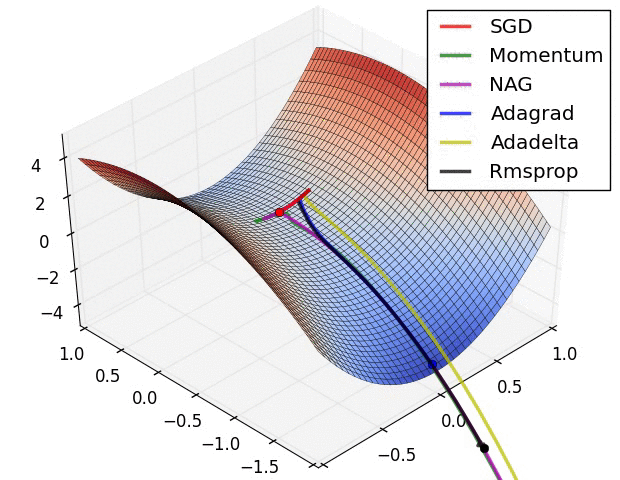
左図:MomentumやNAGではボールのように転がっていく。 右図:RMSpropのようなアルゴリズムは小さい勾配をうまくとらえることができている。 Image Credit: Alec Radford
最近ではAdamをデフォルトとして使えばよいと言われているのですが、ここではDanielさんの記事に合わせてNesterov accelerated gradientを使用します。
また、Kerasのデフォルトの設定を使用したい場合はoptimizerを文字列で指定して、
model.compile(loss='mean_squared_error', optimizer='sgd')
これは
SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False)
と設定したことと等価です。
この問題は回帰なので誤差関数には二乗誤差を表すmean_squared_errorを指定しています。Kerasのデフォルトのミニバッチのサイズは32です。validation_split=0.2の部分ではサンプルのうち20%をバリデーションに割り当てています。出力は以下のようになります。
Train on 1712 samples, validate on 428 samples
Train on 1712 samples, validate on 428 samples
Epoch 1/100
1712/1712 [==============================] - 1s - loss: 0.0559 - val_loss: 0.0160
Epoch 2/100
1712/1712 [==============================] - 1s - loss: 0.0125 - val_loss: 0.0120
Epoch 3/100
1712/1712 [==============================] - 1s - loss: 0.0109 - val_loss: 0.0113
Epoch 4/100
1712/1712 [==============================] - 1s - loss: 0.0099 - val_loss: 0.0093
Epoch 5/100
1712/1712 [==============================] - 1s - loss: 0.0090 - val_loss: 0.0098
…
Epoch 50/100
1712/1712 [==============================] - 1s - loss: 0.0032 - val_loss: 0.0046
Epoch 51/100
1712/1712 [==============================] - 1s - loss: 0.0032 - val_loss: 0.0042
Epoch 52/100
1712/1712 [==============================] - 1s - loss: 0.0031 - val_loss: 0.0043
Epoch 53/100
1712/1712 [==============================] - 1s - loss: 0.0031 - val_loss: 0.0041
Epoch 54/100
1712/1712 [==============================] - 1s - loss: 0.0031 - val_loss: 0.0043
Epoch 55/100
…
Epoch 95/100
1712/1712 [==============================] - 1s - loss: 0.0023 - val_loss: 0.0034
Epoch 96/100
1712/1712 [==============================] - 1s - loss: 0.0022 - val_loss: 0.0034
Epoch 97/100
1712/1712 [==============================] - 1s - loss: 0.0022 - val_loss: 0.0035
Epoch 98/100
1712/1712 [==============================] - 1s - loss: 0.0022 - val_loss: 0.0034
Epoch 99/100
1712/1712 [==============================] - 1s - loss: 0.0022 - val_loss: 0.0034
Epoch 100/100
1712/1712 [==============================] - 1s - loss: 0.0022 - val_loss: 0.0035
結果の確認
学習曲線を表示させてみましょう。TensorFlowをバックエンドとして使用している場合は可視化にTensorBoardを使用することもできますが、ここではMatplotlibを使います。
Kerasではfit()の戻り値としてHistoryオブジェクトが取れるので、これを利用してグラフを描くことができます。保存しておきたい場合は、Pickleを使ってHistoryオブジェクトを保存するのではなく、辞書型であるHistory.historyを保存しておくと良いかと思います。
pyplot.plot(hist.history['loss'], linewidth=3, label='train')
pyplot.plot(hist.history['val_loss'], linewidth=3, label='valid')
pyplot.grid()
pyplot.legend()
pyplot.xlabel('epoch')
pyplot.ylabel('loss')
pyplot.ylim(1e-3, 1e-2)
pyplot.yscale('log')
pyplot.show()
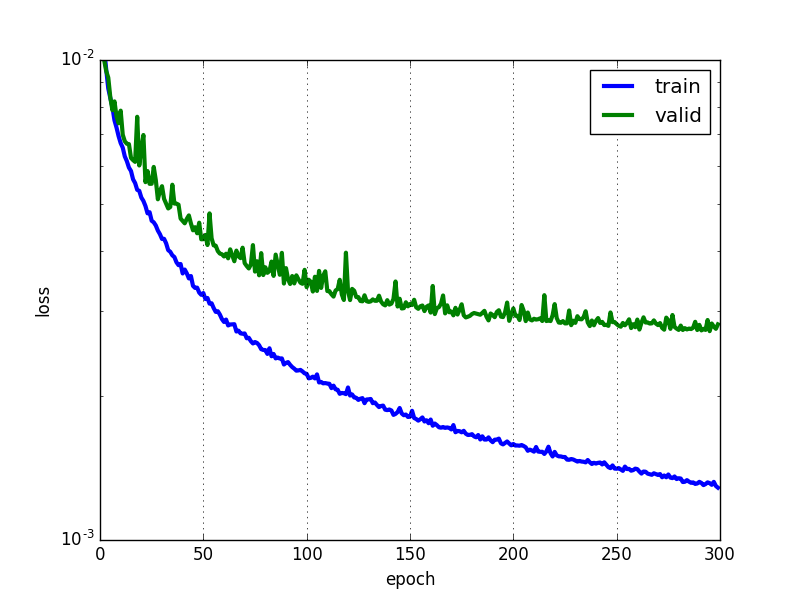
グラフの横軸の単位はエポック(Epoch)です。これは「何回全てのサンプルを見たか」を表しています。1エポックであれば、全てのサンプルが一度見られたということになります。イテレーション数はバッチサイズの影響を受けるため、横軸には一般にエポックが使われます。
このようにグラフの縦軸をLogスケールで表示する場合があります。一般に学習は指数関数のような形で進むので、片対数グラフで表示すると直線的になる傾向があるためです。
図を見ると、訓練誤差(Training Error)に対してバリデーションエラー(Validation Error)が大きく、過学習が起きていることが分かります。ちなみにこのモデルでは中間層のニューロン数は小さく設定してありますが、ここまでは正則化(Regularization)は行っていません。
ちなみにNesterov accelerated gradientと純粋なSGDを比較すると下図のようになります。Nesterov accelerated gradientは純粋なSGDに比べてより早く収束していることが分かります。
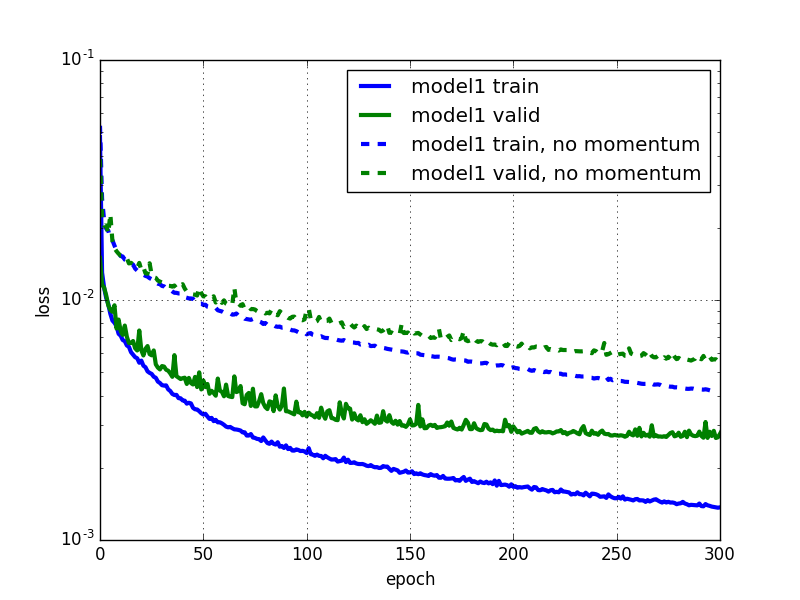
次に、学習済みのモデルを使ってkeypointsを出力し、顔のどのあたりに位置しているか実際に見てみましょう。
from matplotlib import pyplot
X_test, _ = load(test=True)
y_test = model.predict(X_test)
fig = pyplot.figure(figsize=(6, 6))
fig.subplots_adjust(
left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(16):
axis = fig.add_subplot(4, 4, i+1, xticks=[], yticks=[])
plot_sample(X_test[i], y_test[i], axis)
pyplot.show()

ほんの少しズレている部分もありますが、大体うまくプロットできていることが分かります。
ここで学習済みのモデルの保存方法を紹介しておきます。プロットするたびに学習し直すと時間がかかるので、保存しておくと便利です。モデルを保存する際にはpickleやcPickleがよく使われますが、Kerasではこの方法は非推奨となっているため、以下のようにします。
json_string = model.to_json()
open('model1_architecture.json', 'w').write(json_string)
model.save_weights('model1_weights.h5')
model.to_json()の部分では、モデルのアーキテクチャのみをJSONとして出力しています。重みの情報は持っていません。重みも保存したい場合はmodel.save_weights()を使います。保存したモデルを読み込む場合は以下のようになります。
from keras.models import model_from_json
model = model_from_json(open('model1_architecture.json').read())
model.load_weights('model1_weights.h5')
重みを保存するためには事前にh5pyというPythonのライブラリをインストールしておく必要があります。さらにh5pyを入れる前にHDF5を入れておく必要があるので注意が必要です。インストールにはこちらの記事が参考になります。
モデル2:畳み込み
次は畳み込みニューラルネットワーク(Convolutional Neural Network)を使って実装していきたいと思います。畳み込みニューラルネットワークは画像認識で大きな成功を収めているモデルで、畳み込み層(Convolutional Layer)、プーリング層(Pooling Layer)、全結合層(Fully-Connected Layer)からなります。
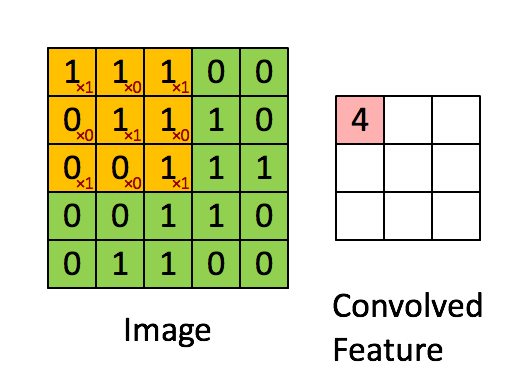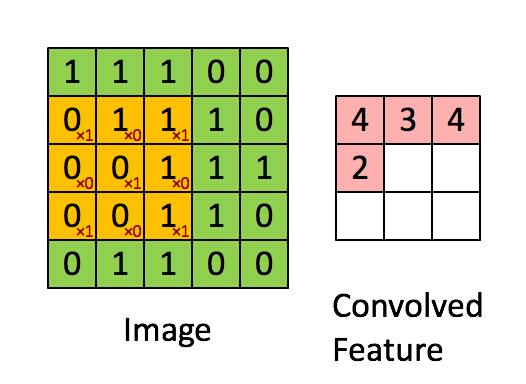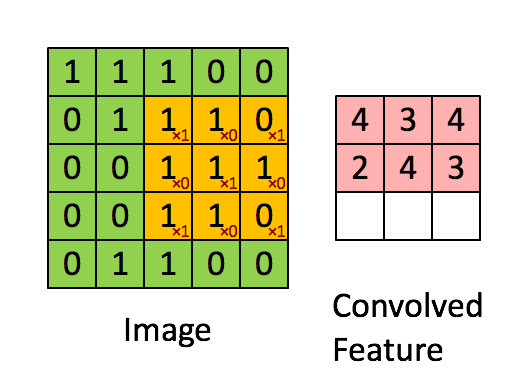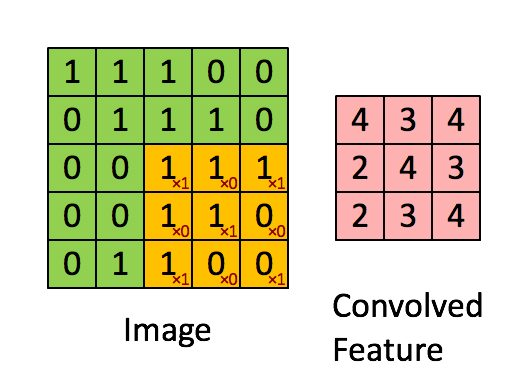
畳み込み層では、入力である画像に対して下図のようにフィルタを当ててスライドしていきます。ここで学習するのは各フィルタの重みで、重みは下図のピンク色のニューロン間で共有されています。普通のニューラルネットワークではニューロンはひとつ前の層の全てのニューロンと繋がっていましたが、ここでは一部とのみ繋がりがあるようになっています。
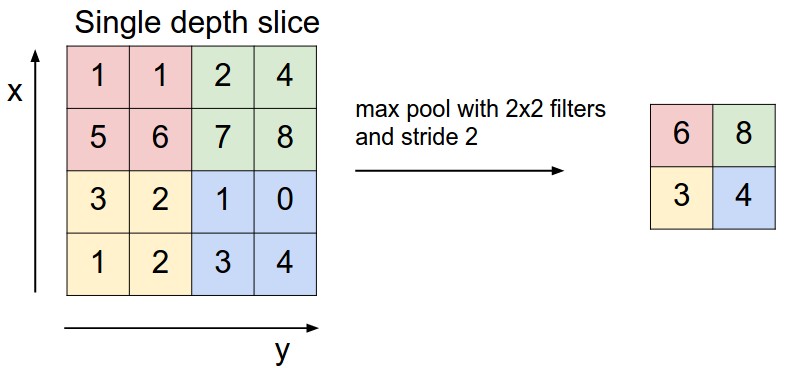
プーリング層の役割はサイズを小さくすることによりパラメータや計算量を減らしたり、過学習を防ぐことです。下図のように最大プーリング(Max Pooling)の場合は、対象となる範囲の最大値を出力します。また、図のように入力に対して出力のサイズは小さくなります。
全結合層では、普通のニューラルネットワークと同じ構造をしていて、ニューロンはひとつ前の層の全てのニューロンと繋がっています。
モデル1では9,216ピクセルからなるベクトルをインプットにしていましたが、ここでは (1, 96, 96) の形に変換します。96は画像の縦横方向のピクセル数を表し、1はチャネルを表します。今回はグレースケールの画像を扱っているのでチャネルは一つしかありません。
この形に変換する便利な関数を用意しておきます。
def load2d(test=False, cols=None):
X, y = load(test, cols)
X = X.reshape(-1, 1, 96, 96)
return X, y
畳み込み層3層と全結合層2層からなる畳み込みニューラルネットワークを構築します。畳み込み層の後に毎回2x2の最大プーリングを行います。フィルタの数は32, 64, 128となっていて、全結合層のニューロン数はどちらも500です。
以下がKerasで書いたコードになります。
from keras.layers import Convolution2D, MaxPooling2D, Flatten
X, y = load2d()
model2 = Sequential()
model2.add(Convolution2D(32, 3, 3, input_shape=(1, 96, 96)))
model2.add(Activation('relu'))
model2.add(MaxPooling2D(pool_size=(2, 2)))
model2.add(Convolution2D(64, 2, 2))
model2.add(Activation('relu'))
model2.add(MaxPooling2D(pool_size=(2, 2)))
model2.add(Convolution2D(128, 2, 2))
model2.add(Activation('relu'))
model2.add(MaxPooling2D(pool_size=(2, 2)))
model2.add(Flatten())
model2.add(Dense(500))
model2.add(Activation('relu'))
model2.add(Dense(500))
model2.add(Activation('relu'))
model2.add(Dense(30))
sgd = SGD(lr='0.01', momentum=0.9, nesterov=True)
model2.compile(loss='mean_squared_error', optimizer=sgd)
hist2 = model2.fit(X, y, nb_epoch=1000, validation_split=0.2)
MaxPooling2Dにはborder_modeという引数があり、パディングを変更することができます。デフォルトは’valid’になっていてパディングはありません。
Flattenは全結合層が読み込めるように (None, 128, 11, 11) の配列を (None, 15488) に変形しています。
また、モデルのアーキテクチャは以下のようにしてモデルを簡単に可視化することができます。
from keras.utils.visualize_util import plot
plot(model2, to_file='model2.png', show_shapes=True)
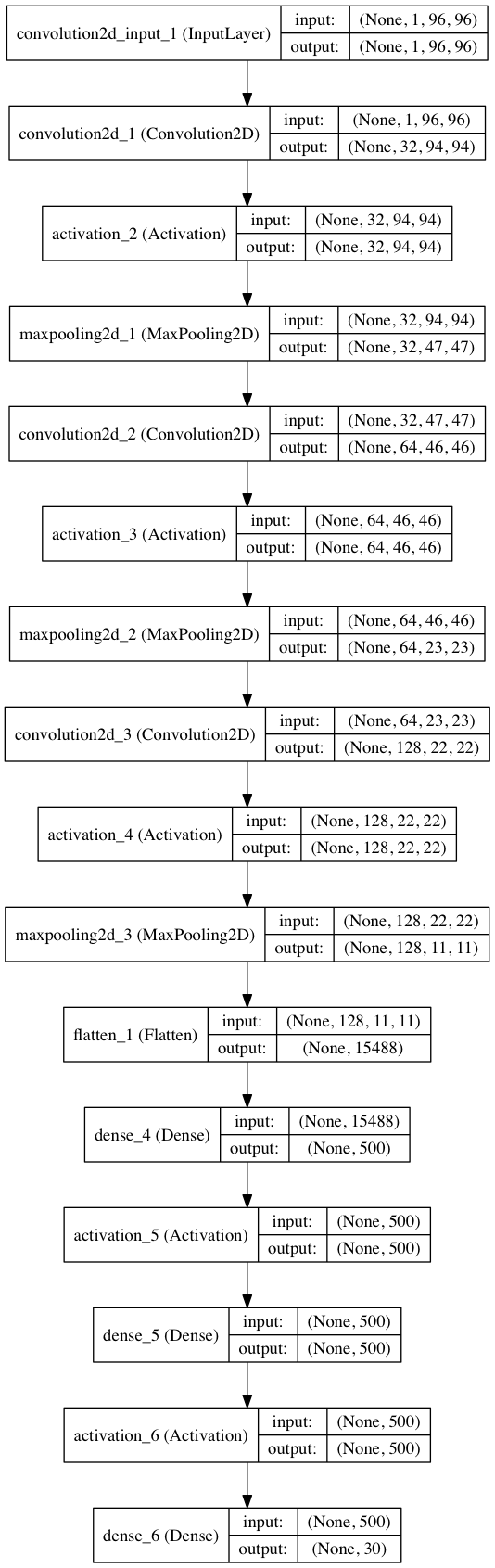
このモデルは層が増えたことなどにより最初のモデルに比べてかなり計算量が多いので、CPUのみだとかなり厳しいです。バックエンドをTheanoにし、AWSのg2.2xlargeというGPUインスタンスで1000エポック計算するのに約40分程度かかりました。1エポックあたり約2秒です。
学習曲線も見てみましょう。
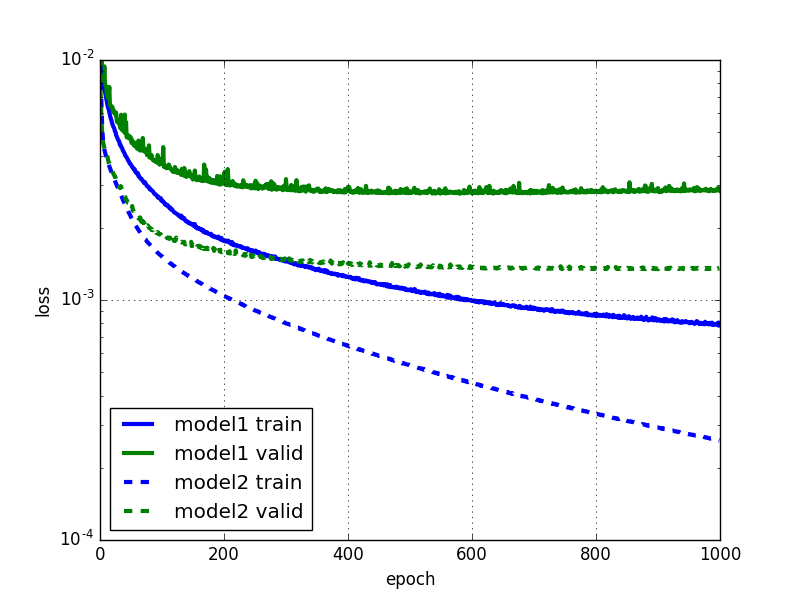
最初のモデルに比べてエラーが小さくなりました。明らかに過学習が起きていますが、このモデルでも重み減衰(Weight Decay)やドロップアウト (Dropout) などの正則化は行っていません。
学習済みのそれぞれのモデルにkeypointを出力させて比較してみましょう。
sample1 = load(test=True)[0][6:7]
sample2 = load2d(test=True)[0][6:7]
y_pred1 = model.predict(sample1)[0]
y_pred2 = model2.predict(sample2)[0]
fig = pyplot.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
plot_sample(sample1, y_pred1, ax)
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
plot_sample(sample2, y_pred2, ax)
pyplot.show()
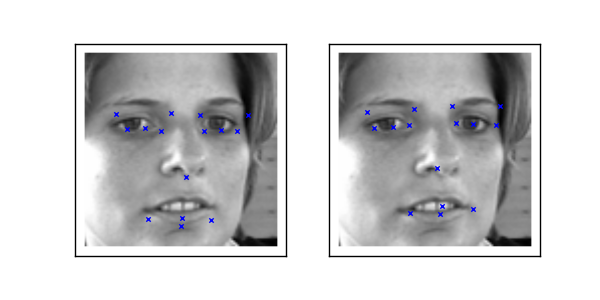
左:model1、右:model2
model2の方がより正確な位置にプロットできている様子が分かります。
Data Augmentation
過学習を防ぐ方法の一つとして、より多くの訓練データを与えるというものがあります。しかし、今回のようにデータが限られていたり、さらに多くのデータを集めるのにコストがかかるといった場合が多いと思います。
そこで、反転・回転させたり、ノイズを入れた画像を生成し、それを訓練データとして使用することを考えます。Data Augmentationには様々な方法がありますが、今回は水平反転のみを行います。
まずはDanielさんの記事と同様に水平方向に反転した画像を表示させてみます。Pythonのスライスを使って簡単に反転させることができます。
X, y = load2d()
X_flipped = X[:, :, :, ::-1]
fig = pyplot.figure(figsize=(6, 3))
ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[])
plot_sample(X[1], y[1], ax)
ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[])
plot_sample(X_flipped[1], y[1], ax)
pyplot.show()

左:元画像、右:水平反転した画像
反転した画像ではkeypointの位置がずれてしまっています。画像を反転させるだけではなく、keypointの位置も変更する必要があることが分かります。どのように変更すればよいでしょうか。
left_eye_center_xとright_eye_center_xはスワップする必要がありますが、nose_tip_yは変更する必要はありません。ここもDanielさんと同様に配列の要素番号を使ってkeypointの方も反転させてみます。
flip_indices = [
(0, 2), (1, 3),
(4, 8), (5, 9), (6, 10), (7, 11),
(12, 16), (13, 17), (14, 18), (15, 19),
(22, 24), (23, 25),
]
df = read_csv(os.path.expanduser(FTRAIN))
for i, j in flip_indices:
print("{} -> {}".format(df.columns[i], df.columns[j]))
出力結果を見ると、期待通りにうまく反転できていることが分かります。
left_eye_center_x -> right_eye_center_x
left_eye_center_y -> right_eye_center_y
left_eye_inner_corner_x -> right_eye_inner_corner_x
left_eye_inner_corner_y -> right_eye_inner_corner_y
left_eye_outer_corner_x -> right_eye_outer_corner_x
left_eye_outer_corner_y -> right_eye_outer_corner_y
left_eyebrow_inner_end_x -> right_eyebrow_inner_end_x
left_eyebrow_inner_end_y -> right_eyebrow_inner_end_y
left_eyebrow_outer_end_x -> right_eyebrow_outer_end_x
left_eyebrow_outer_end_y -> right_eyebrow_outer_end_y
mouth_left_corner_x -> mouth_right_corner_x
mouth_left_corner_y -> mouth_right_corner_y
ここからはKerasでの実装です。KerasにはImageDataGeneratorというクラスがあります。
keras.preprocessing.image.ImageDataGenerator(featurewise_center=False,
samplewise_center=False,
featurewise_std_normalization=False,
samplewise_std_normalization=False,
zca_whitening=False,
rotation_range=0.,
width_shift_range=0.,
height_shift_range=0.,
shear_range=0.,
zoom_range=0.,
channel_shift_range=0.,
fill_mode='nearest',
cval=0.,
horizontal_flip=False,
vertical_flip=False,
dim_ordering='th')
通常は、holizontal_flip=Trueとするだけで簡単に水平反転することができます。
しかし、今回の問題は少し特殊でXを反転させるのに伴いyも適切に反転させる必要があります。そこでImageDataGeneratorを継承したFlippedImageDataGeneratorというクラスを作り、next()をオーバーライドします。
class FlippedImageDataGenerator(ImageDataGenerator):
flip_indices = [
(0, 2), (1, 3),
(4, 8), (5, 9), (6, 10), (7, 11),
(12, 16), (13, 17), (14, 18), (15, 19),
(22, 24), (23, 25),
]
def next(self):
X_batch, y_batch = super(FlippedImageDataGenerator, self).next()
batch_size = X_batch.shape[0]
indices = np.random.choice(batch_size, batch_size/2, replace=False)
X_batch[indices] = X_batch[indices, :, :, ::-1]
if y_batch is not None:
# x座標をフリップ
y_batch[indices, ::2] = y_batch[indices, ::2] * -1
# left_eye_center_x -> right_eye_center_x のようにフリップ
for a, b in self.flip_indices:
y_batch[indices, a], y_batch[indices, b] = (
y_batch[indices, b], y_batch[indices, a]
)
return X_batch, y_batch
単純に反転させた画像をXに追加するのではなく、バッチを取り出すたびに50%の確率で反転させることによってメモリの消費量を抑えることができます。Danielさんによるとこの部分の処理はGPUが処理を行ってる間に実行されるので実質コストはないとのことですが、実際には計算時間が少し伸びるようです。もしかしたらKerasとLasagneの違いもあるのかもしれません。
Generatorを使う場合にはfit()ではなくfit_generator()というメソッドを使用します。
from sklearn.cross_validation import train_test_split
X, y = load2d()
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
model3 = Sequential()
model3.add(Convolution2D(32, 3, 3, input_shape=(1, 96, 96)))
model3.add(Activation('relu'))
model3.add(MaxPooling2D(pool_size=(2, 2)))
model3.add(Convolution2D(64, 2, 2))
model3.add(Activation('relu'))
model3.add(MaxPooling2D(pool_size=(2, 2)))
model3.add(Convolution2D(128, 2, 2))
model3.add(Activation('relu'))
model3.add(MaxPooling2D(pool_size=(2, 2)))
model3.add(Flatten())
model3.add(Dense(500))
model3.add(Activation('relu'))
model3.add(Dense(500))
model3.add(Activation('relu'))
model3.add(Dense(30))
sgd = SGD(lr='0.01', momentum=0.9, nesterov=True)
model3.compile(loss='mean_squared_error', optimizer=sgd)
flipgen = FlippedImageDataGenerator()
hist3 = model3.fit_generator(flipgen.flow(X_train, y_train),
samples_per_epoch=X_train.shape[0],
nb_epoch=3000,
validation_data=(X_val, y_val))
fit_generator()ではvalidation_splitという引数は使えないので、validation_dataに手動でテストデータを与えます。
結果を見てみましょう。水平反転したデータを加えた方(model3)では過学習が軽減されている様子が分かります。また、バリデーションエラーが僅かに小さくなっています。
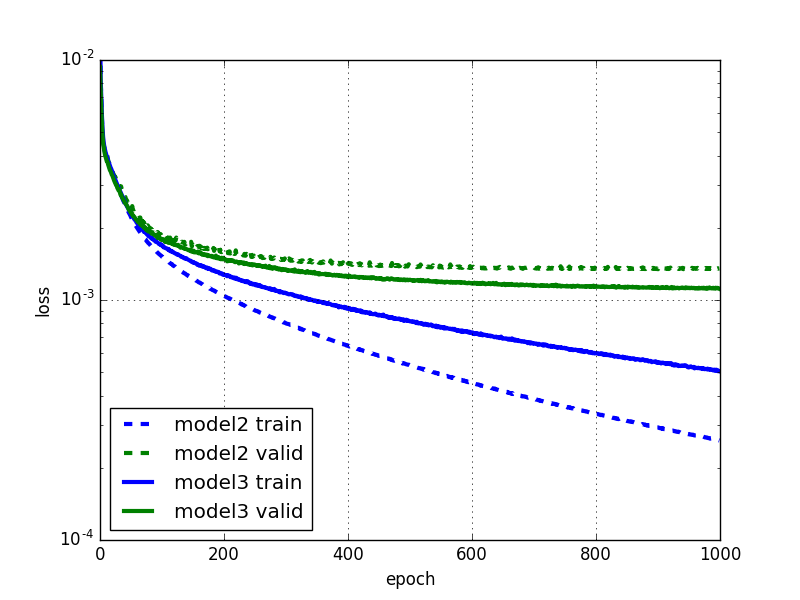
毎回最初から学習し直すのではなく、前回学習した続きから学習したい場合があると思います。 例えば、1000エポックまで学習したモデルを使ってそこからさらに3000エポックまで 計算したいというような場合です。
fit()やfit_generator()を実行する際には重みの初期化は行われないため、続きから学習していくことができます。
model3 = model_from_json(open('model3_architecture.json').read())
model3.load_weights('model3_weights.h5')
model3.compile(loss='mean_squared_error', optimizer=sgd)
flipgen = FlippedImageDataGenerator()
hist3 = model3.fit_generator(flipgen.flow(X_train, y_train),
samples_per_epoch=X_train.shape[0],
nb_epoch=2000,
validation_data=(X_val, y_val))
学習係数の変更
時間とともに学習係数を変化させることによって収束を早めることを考えます。
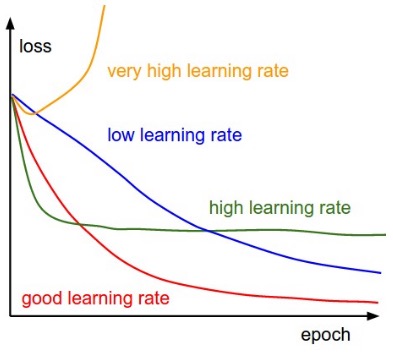
図のように大きな学習係数を用いると学習が速く進みますが、エラーが大きい所で学習が止まってしまいます。これは運動エネルギーが大き過ぎるため、極小値の周りをあちこちふらついてしまっていると考えられます。一方、学習係数が小さい場合は、最終的にはエラーが小さくなりますが、学習に時間がかかります。
そこで、直感的には大きな学習係数からスタートし、徐々に学習係数を小さくしていくことによって効率よく学習できると考えられます。Kerasでは
sgd = SGD(lr=0.1, decay=1e-6, momentum=0.9, nesterov=True)
のようにdecayというハイパーパラメータを設定することによって学習係数を非線形に小さくしていくことができます。ですが、ここではDanielさんと同様に、最初と最後の学習係数を指定し、エポックとともに線形に変化させていくことにします。
from keras.callbacks import LearningRateScheduler
start = 0.03
stop = 0.001
nb_epoch = 1000
learning_rates = np.linspace(start, stop, nb_epoch)
# ...
# 畳み込み層やプーリング層はmodel3と同様
# ...
change_lr = LearningRateScheduler(lambda epoch: float(learning_rates[epoch]))
sgd = SGD(lr=start, momentum=0.9, nesterov=True)
model4.compile(loss='mean_squared_error', optimizer=sgd)
flipgen = FlippedImageDataGenerator()
hist4 = model4.fit_generator(flipgen.flow(X_train, y_train),
samples_per_epoch=X_train.shape[0],
nb_epoch=nb_epoch,
validation_data=(X_val, y_val),
callbacks=[change_lr])
Kerasで学習係数を変更するのにはLearningRateSchedulerを使用します。コールバックを自分で書けばモメンタムも時間とともに変化させることができそうですが、Kerasではデフォルトでは学習係数しか変更できないため、ここでは学習係数のみを変更します。
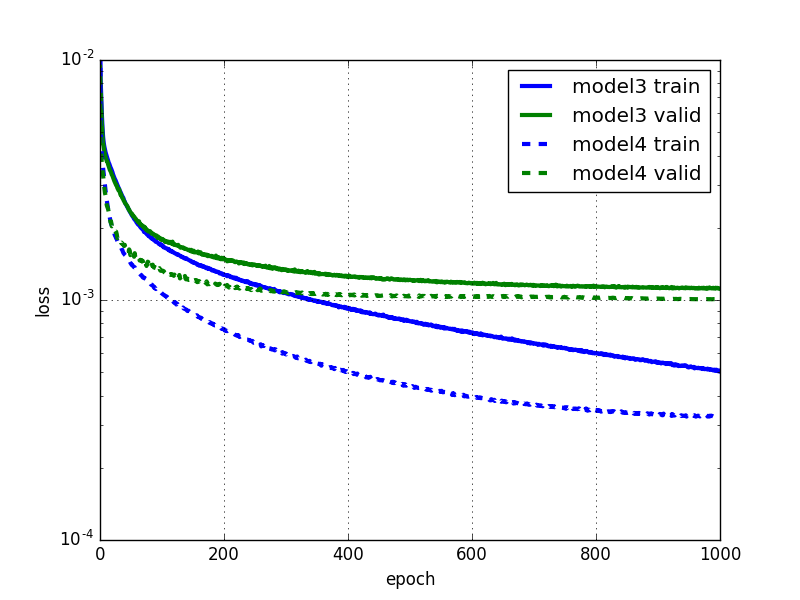
学習係数を変化させた場合(model4)の方がより速く学習が進み、かつバリデーションエラーをさらに低くできていることが分かります。
ドロップアウト
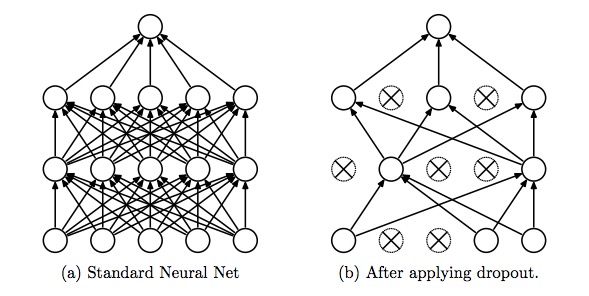
ドロップアウトは、過学習を防ぐ非常に有効かつシンプルな手法で、近年よく使われます。図のように一定の確率でランダムにニューロンを無視して学習を進めます。
アンサンブルと言って、複数の独立したモデルを使って予測を行うと、一般により良い結果が得られることが知られています。単純には、各モデルはそれぞれ異なった過学習をしているので、平均を取ることによって過学習を防いでいると考えられます。
ドロップアウトは、ランダムにニューロンを無視することによって、非常に多くの異なるニューラルネットワークを学習させていると解釈することができます。これによって過学習を防いでいると考えられます。
また、ドロップアウトが適用されるのは学習時のみで、テスト時には適用されません。
コードは以下のようになります。分かりやすいようにmodel4から変更した部分に# !というコメントを付けました。
from keras.layers import Dropout # !
start = 0.03
stop = 0.001
nb_epoch = 1000
X, y = load2d()
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
model5 = Sequential()
model5.add(Convolution2D(32, 3, 3, input_shape=(1, 96, 96)))
model5.add(Activation('relu'))
model5.add(MaxPooling2D(pool_size=(2, 2)))
model5.add(Dropout(0.1)) # !
model5.add(Convolution2D(64, 2, 2))
model5.add(Activation('relu'))
model5.add(MaxPooling2D(pool_size=(2, 2)))
model5.add(Dropout(0.2)) # !
model5.add(Convolution2D(128, 2, 2))
model5.add(Activation('relu'))
model5.add(MaxPooling2D(pool_size=(2, 2)))
model5.add(Dropout(0.3)) # !
model5.add(Flatten())
model5.add(Dense(500))
model5.add(Activation('relu'))
model5.add(Dropout(0.5)) # !
model5.add(Dense(500))
model5.add(Activation('relu'))
model5.add(Dense(30))
change_lr = LearningRateScheduler(lambda epoch: float(learning_rates[epoch]))
sgd = SGD(lr=start, momentum=0.9, nesterov=True)
model5.compile(loss='mean_squared_error', optimizer=sgd)
flipgen = FlippedImageDataGenerator()
hist5 = model5.fit_generator(flipgen.flow(X_train, y_train),
samples_per_epoch=X_train.shape[0],
nb_epoch=nb_epoch,
validation_data=(X_val, y_val),
callbacks=[change_lr])
結果は以下になります。
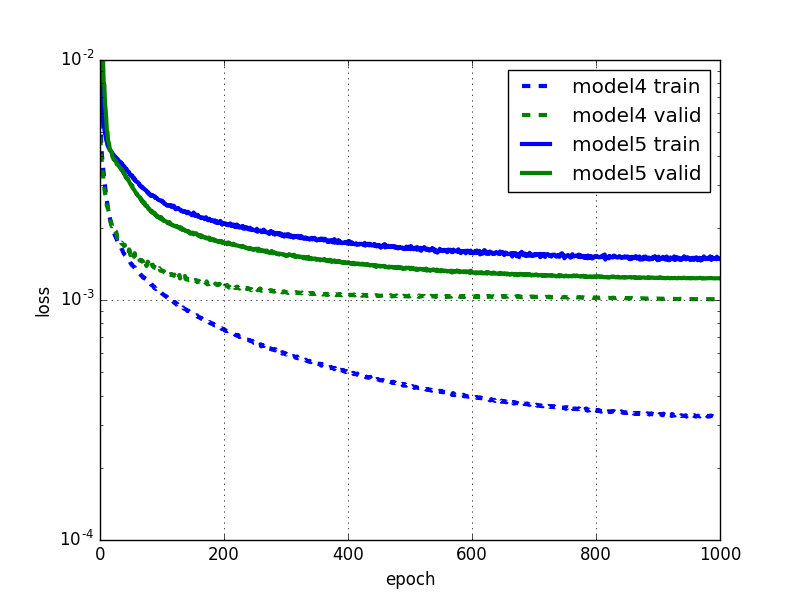
ドロップアウトを行うと収束に時間がかかるようになります。また、model5ではバリデーションエラーよりも訓練誤差の方が大きくなっているように見えます。この訓練誤差にはドロップアウトが含まれていますが、バリデーションエラーの方にはドロップアウトが含まれていないことに注意する必要があります。
ドロップアウトなしの状態での訓練誤差は以下のようにして計算することができます。
from sklearn.metrics import mean_squared_error
print('mean squared error', mean_squared_error(model5.predict(X), y))
# 結果 ('mean squared error', 0.001113090048747249)
訓練誤差が0.00111がであるのに対しバリデーションエラーは0.00123です。訓練誤差とバリデーションエラーの値が近く、ドロップアウトによって過学習を防げているようです。
ドロップアウトよって過学習を防げるようになったので、さらにニューロンの数を増やすことができそうです。全結合層のニューロンの数を500から1000に増やし、5000エポックまで計算してみましょう。
# ...
nb_epoch = 5000
# ...
model6.add(Flatten())
model6.add(Dense(1000))
model6.add(Activation('relu'))
model6.add(Dropout(0.5))
model6.add(Dense(1000))
model6.add(Activation('relu'))
model6.add(Dense(30))
# ...
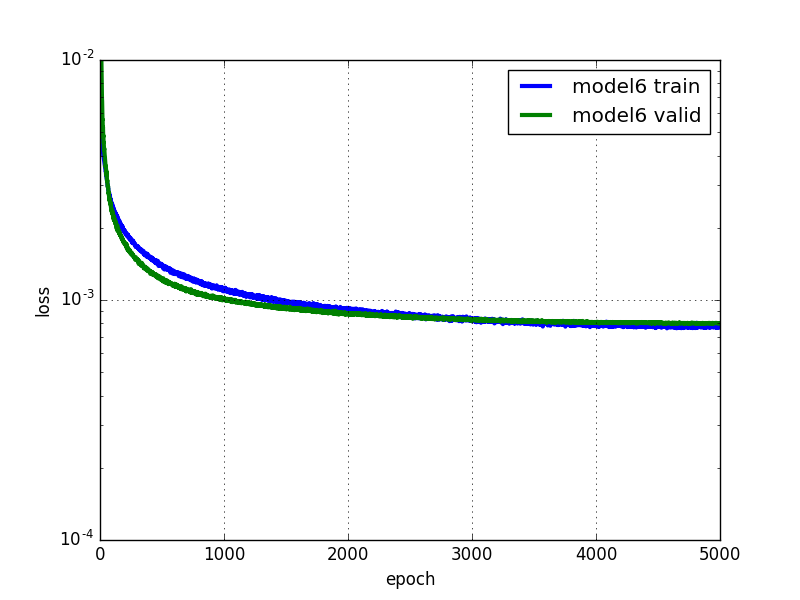
バリデーションエラーは0.0008とこれまでで最も低い値になりました。計算を続けるともっとエラーが下がっていきそうですが、5000エポックまでで既に6時間程度計算に時間がかかっているのでここまでにしておきたいと思います。
Early Stopping
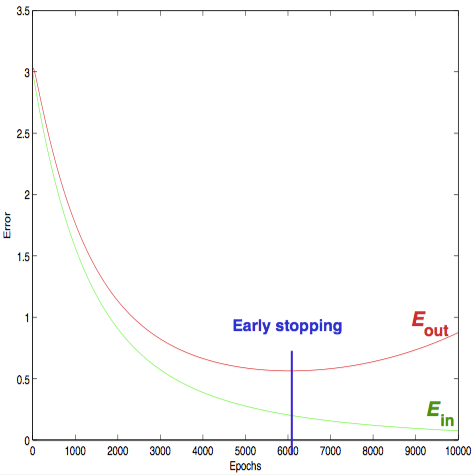
ここで簡単にEarly Stoppingという手法を簡単に紹介しておきます。
図のように過学習が進んでいくと、バリデーションエラーは減少から増加に転じます。そのため、バリデーションエラーが最小になった所で学習をストップさせてしまえば良いと考えられます。
Kerasでは以下のように非常に簡単に実装することができます。
from keras.callbacks import EarlyStopping
early_stop = EarlyStopping(patience=100)
model7.fit_generator(flipgen.flow(X_train, y_train),
samples_per_epoch=X_train.shape[0],
nb_epoch=nb_epoch,
validation_data=(X_val, y_val),
callbacks=[change_lr, early_stop])
patienceというのは「何回連続でエラーの最小値が更新されなかったらストップさせるか」という値です。図のように滑らかに変化してくれればよいのですが、実際にはこれまでに見てきたようにでこぼこしています。また、極小付近にいるだけで、最小となる場所はもっと先にある可能性もあります。そのため、増加に転じたら直ぐにストップさせてしまうのではなく、patienceを与えます。
Kerasではデフォルトでpatience=0に設定されていますが、これだと直ぐに学習がストップしてしまうので、適当な大きさに設定しておくのがよいかと思います。
最終的に使用する重みは、学習をストップさせた時点ではなく、エラーが最小になった時点のものを使用した方が良いはずですが、(現時点では)Kerasはそうなっていないようです。
モデルの特化
ここまで訓練データの約70%を捨てたまま学習を進めてきました。ここではそれらのデータもうまく活用することを考えます。
left_eye_center と right_eye_center を予測するモデル、nose_tip だけを予測するモデルというように特定のkeypointsだけを予測するモデルに分けることによってデータを有効に活用します。
Keypointによって存在するデータ数はばらばらでしたが、データ数が近い一部のkeypointsだけを予測するモデルに分けることによって、有効にデータを活用できるようになります。
Danielさんの記事と同様に6つのモデルに分けてみます。
SPECIALIST_SETTINGS = [
dict(
columns=(
'left_eye_center_x', 'left_eye_center_y',
'right_eye_center_x', 'right_eye_center_y',
),
flip_indices=((0, 2), (1, 3)),
),
dict(
columns=(
'nose_tip_x', 'nose_tip_y',
),
flip_indices=(),
),
dict(
columns=(
'mouth_left_corner_x', 'mouth_left_corner_y',
'mouth_right_corner_x', 'mouth_right_corner_y',
'mouth_center_top_lip_x', 'mouth_center_top_lip_y',
),
flip_indices=((0, 2), (1, 3)),
),
dict(
columns=(
'mouth_center_bottom_lip_x',
'mouth_center_bottom_lip_y',
),
flip_indices=(),
),
dict(
columns=(
'left_eye_inner_corner_x', 'left_eye_inner_corner_y',
'right_eye_inner_corner_x', 'right_eye_inner_corner_y',
'left_eye_outer_corner_x', 'left_eye_outer_corner_y',
'right_eye_outer_corner_x', 'right_eye_outer_corner_y',
),
flip_indices=((0, 2), (1, 3), (4, 6), (5, 7)),
),
dict(
columns=(
'left_eyebrow_inner_end_x', 'left_eyebrow_inner_end_y',
'right_eyebrow_inner_end_x', 'right_eyebrow_inner_end_y',
'left_eyebrow_outer_end_x', 'left_eyebrow_outer_end_y',
'right_eyebrow_outer_end_x', 'right_eyebrow_outer_end_y',
),
flip_indices=((0, 2), (1, 3), (4, 6), (5, 7)),
),
]
このSPECIALIST_SETTINGSという辞書を使ってループを回し、次々に学習させていきます。
Kerasでの実装は以下のようになります。
from collections import OrderedDict
def fit_specialists():
specialists = OrderedDict()
start = 0.03
stop = 0.001
nb_epoch = 10000
for setting in SPECIALIST_SETTINGS:
cols = setting['columns']
X, y = load2d(cols=cols)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
model8 = model_from_json(model7.to_json()) # アーキテクチャのみを取り出す
model8.layers.pop() # 出力層を取り除く
model8.outputs = [model8.layers[-1].output]
model8.layers[-1].outbound_nodes = []
model8.add(Dense(len(cols))) # 新しい出力層を追加
sgd = SGD(lr=start, momentum=0.9, nesterov=True)
model8.compile(loss='mean_squared_error', optimizer=sgd)
plot(model8, to_file="model8_{}.png".format(cols[0]), show_shapes=True)
flipgen = FlippedImageDataGenerator()
flipgen.flip_indices = setting['flip_indices']
early_stop = EarlyStopping(patience=100)
learning_rates = np.linspace(start, stop, nb_epoch)
change_lr = LearningRateScheduler(lambda epoch: float(learning_rates[epoch]))
print("Training model for columns {} for {} epochs".format(cols, nb_epoch))
hist8 = model8.fit_generator(flipgen.flow(X_train, y_train),
samples_per_epoch=X_train.shape[0],
nb_epoch=nb_epoch,
validation_data=(X_val, y_val),
callbacks=[change_lr, early_stop])
specialists[cols] = model8
各モデルのアーキテクチャは基本的にmodel7と同じですが、出力層は変更する必要があります。出力の数を各モデルに対応するkeypoint数に合わせてやる必要があるためです。
ここでは、最後の層(出力層)を取り除いた後、新しく層を追加することによって出力層を変更しています。keras.utils.visualize_util.plot() の出力画像を見ると、出力層がちゃんと変更されていることを確認できます。
転移学習
複数の特化したモデルに分けて学習させることによってデータを有効に活用にできるようになりました。しかし、データ数とモデル数が増えたことで、学習に非常に時間がかかるようになってしまいました。
そこで転移学習(Transfer Learning)を使うことを考えます。転移学習では既に学習済みの重みを初期値として使用します。初めから学習するのに比べて、学習時間を大幅に短縮することが期待できます。
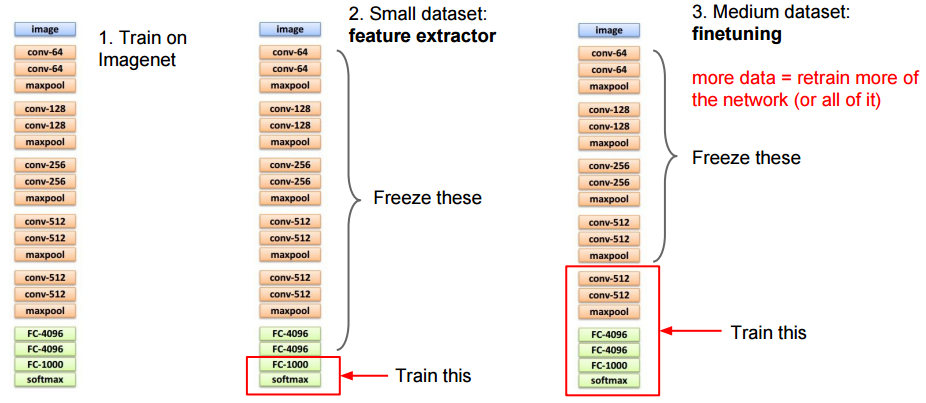
転移学習には様々なパターンがあります。下図のように畳み込み層をフリーズさせて(重みを更新しないで)全結合層のみを学習させるパターンや、畳み込み層も含めて全ての層で学習を行うパターンなどがあります。
どのパターンを使うべきかは、①新しく学習に使用するデータの量、②事前の学習に使用したデータと新しいデータが似ているか、によります。例えば、新しいデータ量が少なく、そして事前学習に使用したデータと似ている場合は、過学習を防ぐために畳み込み層はフリーズさせてしまえばよく、全結合層のみを学習します。畳み込み層は純粋に特徴量を抽出するだけの働きをすることになります。
新しいデータが異なる場合はどうでしょうか。そのような場合でも、畳み込み層の低い層は共通して使える可能性が高いため、低い層だけをフリーズさせ、その先の層だけを学習させることができます。
今回のように新しいデータが多く(約70%のデータを捨てていました)、かつ事前学習に使用したデータと似ている場合には、全ての層で学習するのがよいと思われます。過学習に陥る可能性が低いからです。ここでは全結合層の最後の層のみを新しい層と入れ替え、フリーズさせることなく全ての層で学習を行います。
# ...
def fit_specialists(fname_pretrain=None):
specialists = OrderedDict()
for setting in SPECIALIST_SETTINGS:
cols = setting['columns']
X, y = load2d(cols=cols)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
model8 = model_from_json(model7.to_json())
if fname_pretrain:
model8.load_weights(fname_pretrain) # 事前に学習した重みを読み込む
model8.layers.pop()
model8.outputs = [model8.layers[-1].output]
model8.layers[-1].outbound_nodes = []
model8.add(Dense(len(cols)))
model7と同じアーキテクチャを持つモデルを構築し、ファイルに保存しておいた重みを読み込ませます。出力層を入れ替えた際に、出力層部分の重みだけランダムに初期化されているはずです。
この条件で実行してみます。
start = 0.01
stop = 0.001
nb_epoch = 300
本当はもっと長く学習させたいのですが、かなり時間がかかるので今回は300エポックにしてみました。これだけでもGPUを使用して5時間くらいかかっています。また、開始時の学習係数はこれまでよりも少し小さい0.01に設定してあります。転移学習によって(出力層以外は)既にある程度学習が進んだ状態から始まるため、少し小さめの学習係数の方がよいだろうと考えたからです。初期値として使用する重みとしては5000エポックまで計算しているmodel6のものを使用しました。
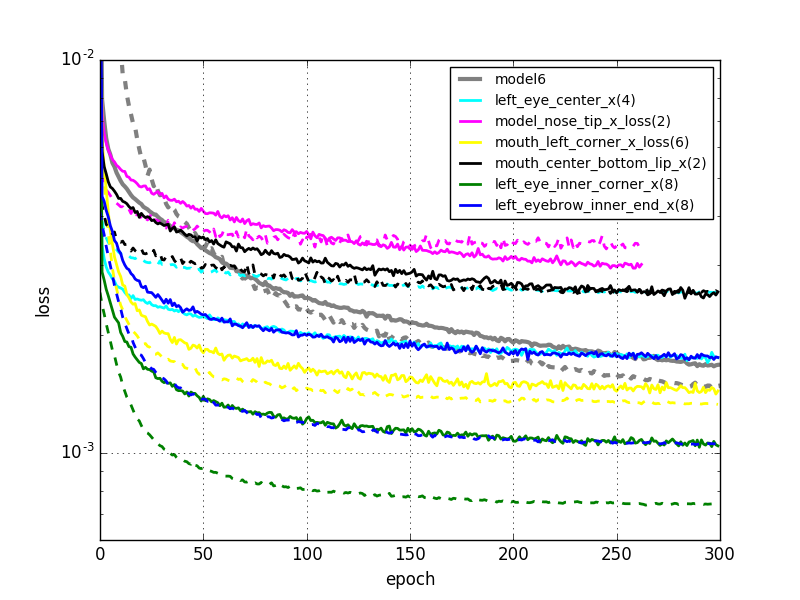
実線:訓練誤差。点線:バリデーションエラー
6つのモデルの学習曲線に加えて、比較のためにmodel6の学習曲線も載せておきました(model6は5000エポックまで計算しているので、各エポックにおける学習係数はmodel8とは異なります)。
この記事ではこれが最後のモデルになりますが、まだまだ改善の余地があります。例えば、学習が進んでいる出力層以外の層の学習係数を小さくする方法が考えられます。または、学習の初期段階において新しく入れ替えた出力層の勾配が他と比べて大きいはずなので、その他の層を始めはフリーズさせておいて、途中から全ての層を学習するように切り替えることによって効率よく学習させる方法などが考えられます(ちなみにKerasでもフリーズさせることができます)。
また、学習曲線を見ると特化したモデル毎に過学習の度合いが異なっていたりするので、ドロップアウト率などのパラメータを調整することでさらに改善していくことができるはずです。
まとめ
中間層が1層の普通のニューラルネットワークから始まり、Data augmentationや転移学習を用いた畳み込みニューラルネットワークを複数構築するところまで来ました。最終的なモデルをKerasで実装したコードはこちらで確認することができます。
Kerasはレゴブロックを組み合わせるかのようにして、簡単にディープラーニングのモデルを作成できる便利なライブラリです。これを使って楽しく開発できるのではないかと思います。
参考文献
- Using convolutional neural nets to detect facial keypoints tutorial
- Keras Documentation
- CS231n Convolutional Neural Networks for Visual Recognition
- Srivastava et al. 2014. Dropout: A Simple Way to Prevent Neural Networks from Overfitting
- Neural Networks and Deep Learning
- An overview of gradient descent optimization algorithms
- Coursera, Stanford Machine Learning
- Caltech, Learning from Data