DQNをKerasとTensorFlowとOpenAI Gymで実装する

はじめに

少し時代遅れかもしれませんが、強化学習の手法のひとつであるDQNをDeepMindの論文Mnih et al., 2015, Human-level control through deep reinforcement learningを参考にしながら、KerasとTensorFlowとOpenAI Gymを使って実装します。

前半では軽くDQNのおさらいをしますが、少しの強化学習の知識を持っていることを前提にしています。
すでにいくつか良記事が出ているので紹介したいと思います。合わせて読むと理解の助けになると思うので、是非参考にしてみてください。

DQNの生い立ち　＋　Deep Q-NetworkをChainerで書いた
DQNが生まれた背景について説明してくれています。Chainerでの実装もあるそうです。
ゼロからDeepまで学ぶ強化学習
タイトルの通り、ゼロからDeepまでさらっと学べます。こちらもChainerでの実装があるそうです。

また、強化学習を一からがっつり勉強したいという方へのソースもいくつか紹介したいと思います。

RL Course by David Silver at UCL
DeepMindのDavid Silver氏のUCLでの講義。強化学習の基礎知識はこれでだいたい身に付きます。動画とスライドがあります。
Reinforcement Learning: An Introduction
言わずと知れた強化学習の教科書。原著は無料で読めます。日本語版もありますがこちらは有料です。

おさらい

自分への復習も兼ねて、DQNまでの強化学習の基礎をおさらいしたいと思います。別に大丈夫という方は実装まで飛ばしてもらえればと思います。

強化学習（Reinforcement Learning）

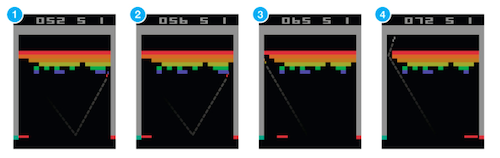
Atariのブロック崩し（Mnih et al., 2015）

ブロック崩しをAIにプレイさせることを考えます。入力はゲーム画面で、出力はバーの移動（右移動とか左移動とか）にすれば、分類で解けそうな感じがします。
でもそれだとたくさんの教師データが必要になりそうなので、事前に何百万回もゲームをプレイして集めないといけないです。ちょっと面倒くさいですね。

ここで強化学習の登場です。強化学習は教師あり学習とも教師なし学習とも少し違います。「さっきのあのプレイ、よかったんじゃない？」のような感じで、時間差のフィードバックである「報酬」（ゲームスコア）を元に、環境（ブロック崩し）の中でどう振る舞えばいいのかを学習します。

しかし強化学習は一見簡単そうで、実はいくつかチャレンジングな問題もあります。

貢献度分配問題（Credit Assignment Problem）
ブロックを消してスコアが上がり、報酬をもらえたとします。しかし実際には、その報酬に貢献したファインプレイはもっと前の、バーでボールを跳ね返したときですよね。でもそのときにもらえる報酬は0。

「知識利用」と「探査」のジレンマ(Explore-Exploit Dilemma)
シンプルな戦略として、バーを両端のどちらかに置いていれば、ゲームオーバーまでに一回はボールを跳ね返してブロックを消し報酬がもらえるということが既に分かっていたとします。この戦略を取り続けるべきか？それともより多くの報酬を期待して違う行動を取ってみるべきか？

マルコフ決定過程（Markov Decision Process）

強化学習を考えやすい枠組みに落とし込むときには、一般的にマルコフ決定過程（MDP）として問題を設定します。

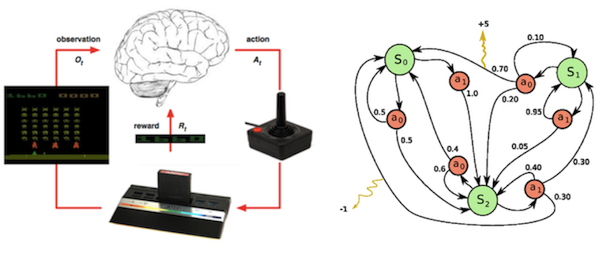
左: 強化学習の問題（Lecture 1: Introduction to Reinforcement Learning at UCL)　右: マルコフ決定過程（Wikipedia）

ブロック崩し（環境）をしているとすると、自分はゲーム画面（バーの位置、ボールの位置・方向、残ってるブロックの数）（状態）を見て、バーを移動（行動）させますね。ときにはそれがスコアの増加（報酬）に繋がることもあります。

上記のプロセスを繰り返すことで、状態$ s $と行動$ a $、報酬$ r $のセットが得られます。

$s_{0}, a_{0}, r_{1}, s_{1}, a_{1}, r_{2}, s_{2}, ..., s_{n-1}, a_{n-1}, r_{n}, s_{n}$

これがMDPでの強化学習の設定になります。つまり、状態を観測し、行動をすると、環境の中で状態が確率的に遷移し、環境から確率的に報酬が得られるというものです。

またMDPはマルコフ性を持っていて、これは次の状態$ s_{t+1} $は一時刻前の状態$ s_{t} $と行動$ a_{t} $だけによって決まるということです。つまり、現在の状態と行動から、次の時刻の状態と報酬を予測することができます。さらに繰り返し計算により、すべての将来の状態と報酬を予測することができるようになるわけです。

割引率を用いた累積報酬(Discounted Future Reward)

強化学習のゴールは、環境から得られる最終的な累積報酬を最大化することです。要はたくさんブロックを消して、ゲームをクリアしたいということです。また賢い戦略として、短期的な報酬だけを考えるのではなくて、長期的な報酬も視野に入れます。しかし、長期的な報酬は本当に手に入るか分かりません。そこで、0から1の値をとる割引率$ \gamma $を用いることで、各時刻での報酬に重み付けをします（累積報酬が発散しないようするためでもあります）。

ある時刻$ t $での、将来得られる累積報酬は

$R_{t} = r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + ... + \gamma^{n-t-1} r_{n}$

これは

$R_{t} = r_{t+1} + \gamma (r_{t+2} + \gamma (r_{t+3} + ...)) = r_{t+1} + \gamma R_{t+1}$

となりますね。この累積報酬の最大化を常に考えることになります。

行動価値関数(Action-Value Function)

強化学習では、状態$ s $において行動$ a $を取ることがどのぐらい良いのかを測る関数があります。

$Q(s_{t}, a_{t}) = \mathbb{E} \left[ R_{t}|s_{t}=s, a_{t}=a \right]$

期待値で表されていますが、「どのくらい良いのか」ということを、先程出てきた将来にわたって得られる累積報酬によって定義しています。

Q学習(Q-Learning)

各状態において、可能な行動の中で最も行動価値関数の値が高い行動をとるように学習を行う方法をQ学習と呼びます。

そのような最適な行動価値関数は

$Q^{*} (s, a) = \text{max}Q(s, a)$

となります。これはつまり、状態$ s $において行動$ a $を取り、その後最適な行動をし続けたときの累積報酬の期待値を表しています。これはQ関数と呼ばれ、状態$ s $における行動$ a $のクオリティを表します。

このQ関数を用いて

$\pi^{*} (s) = \text{argmax}_{a}Q^{*} (s, a)$

となるような最適方策$ \pi^{*} (s) $（方策：行動選択のルール）に従い行動する、つまり、$ Q^{*} (s, a) $が最大になる行動を選択することで、最終的な累積報酬を最大化できることになります。

では、現在の状態$ s $と行動$ a $だけ分かっていて、その後の行動や得られる報酬がわかっていない状況で、どうやってそのようなQ関数を求めればいいでしょうか？一つの遷移$ (s, a, r, s’) $に着目すると、状態$ s $で行動$ a $を取るときは

$Q(s, a) = r + \gamma \text{max} _{a'}Q(s', a')$

となります。これはBellman方程式と呼ばれていて、状態$ s $と行動$ a $の最大累積報酬は、すぐに得られる報酬$ r $と次の状態$ s’ $での最大累積報酬の和ということを表しています。

実際にはQ学習では、Q関数をテーブル関数として表し、Bellman方程式を用いてすべての状態行動対$ (s, a) $について、次の式で反復的にQ関数を更新しながら求めていきます。

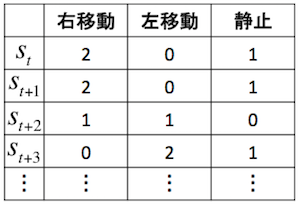
Q-Tableの例

$Q(s, a) ← Q(s, a) + \alpha (r + \gamma \text{max} _{a'}Q(s', a') - Q(s, a))$

$ \alpha $は学習率を表します。この更新式は、状態$ s $において行動$ a $を取る$ Q(s, a) $よりも、行動$ a $を取ったあとの次の状態$ s’ $での最大累積報酬$ r + \gamma \text{max} _{a’}Q(s’, a’) $の方が大きければ、$ Q(s, a) $を大きくし、小さければ$ Q(s, a) $も小さくするということを示しています。つまり、$ Q(s, a) $を$ r + \gamma \text{max} _{a’}Q(s’, a’) $に近づけていくことになります。そして、学習を反復するにつれて、Q関数は真のQ値に近づいていきます。

$ \epsilon $-greedy法

先程のQ学習では、Q値が最も高い行動を選択すればよいと言いましたが、実際には、常にQ値が最大のものだけを選んでいると、（最初はQ値が真の値ではないので、）最初にランダムに与えたQ値の影響が大きく、学習がうまくいきません。そこで、時折ランダムに行動を選択することで、それを解消します。

$ \epsilon $-greedy法はある一定の確率$ \epsilon $でランダムに行動選択をし、それ以外（$ 1-\epsilon $の確率）でQ値が最も高い行動を選択します。

Deep Q-Network

先程はすべての状態と行動についてのQ値のテーブル関数を作ると言いました。しかし、今回のような状態がゲーム画面という高次元のものになると、すべての状態行動対のQ値を求めるには状態数が多すぎで、これではQ関数が収束するのに時間がかかりすぎます。

ここでディープラーニングが登場します。ニューラルネットワークはそのような高次元のデータを取り扱うのに長けているので、Q関数をパラメータ$ \theta $を持つニューラルネットワークで近似することを考えます。つまり、入力に状態であるゲーム画面を取り、出力としてその状態におけるそれぞれの行動に対するQ値を出してもらえればいいわけです。するとこれはただの回帰問題ということになるので、二乗誤差で最適化することができます。

$L = \frac{1}{2} \mathbb{E} \left[ (r + \gamma \text{max} _{a'}Q _{\theta}(s', a') - Q _{\theta}(s, a))^{2} \right]$

ここで、$ r + \gamma \text{max} _{a’}Q _{\theta}(s’, a’) $が教師信号で、$ Q _{\theta}(s, a) $を最適化対象として予測していくことになります。

Q関数近似の問題点

強化学習では、ニューラルネットワークのような非線形関数を使ったQ関数の近似は、一般的に不安定で発散してしまうことが知られています。これにはいくつかの原因があります。ひとつは、観測するデータが連続であり、それらデータ間の相関が高いこと。また、Q関数の小さな更新が方策（行動選択のルール）を大きく変え、それによって観測するデータの分布が大きく変わってしまうこと。さらに、教師信号と予測するQ関数の相関が高いこと。これらを解決するためにいくつかの手法が使われています。

Experience Replay
過去の遷移$ (s, a, r, s’) $のセットを保存しておいて、そこからランダムサンプリングし、ミニバッチとしてネットワークの重みの更新に利用するというものです。これによって、学習データ間の相関をばらばらにし、またプレイヤーの振る舞い（行動の分布）を過去にわたって平均化することができるため、パラメータが振動・発散するのを防ぐことができます。
Target Network
教師信号のQ値を出力するためのTarget Networkを作り、Q Networkのパラメータを定期的にTarget Networkにコピーし、次の更新まで固定します。つまり、古いパラメータを使って教師信号を作ることになります。これにより、Q Networkの更新とTarget Networkの更新との間に時間差が生まれ、学習がうまく進むようになります。

実装

DQNはQ関数をディープなニューラルネットワークにしたものでした。それには畳み込みニューラルネットワーク（CNN）を使っていて、ゲーム画面を状態$ s $として入力し、それぞれのゲーム操作$ a $の行動価値$ Q(s, a;\theta) $を出力します。

また、Mnih et al., 2015では学習をよりうまく進めるためにいくつかの手法を使っています。それらも含めて、できるだけ流れに沿ってコードを解説していきたいと思います。

なお、私のコードには非効率な面も多く見受けられると思いますが、まだまだ精進中の身でありますので、暖かいアドバイスをいただければと思います。全ソースコードはこちらに置いてあります。

全体のアルゴリズム

それぞれの細かい説明に入る前にざっと全体像を俯瞰してみたいと思います。今回実装するDQNのアルゴリズムはこのような感じです。

DQNのアルゴリズム

この流れを頭に入れておけば、これから説明するものも、どこの何のことを言っているのかが分かると思います。

前処理

Atariのゲーム画面は210×160ピクセルのRGBですが、これをこのまま入力とするには計算コストとメモリの面で効率的ではありません。そこで前処理として、ゲーム画面をグレースケールに変換し、84×84ピクセルにリサイズします。

また、一つ前のフレームと現在のフレームの各ピクセルごとに最大値を取ります。これは、Atariのゲームは同時に表示できるスプライトの数に制限があり、偶数または奇数フレームにしか出現しないオブジェクトがあるためです。

状態$ s $

前処理を施したゲーム画面の直近4フレーム分を合わせて状態$ s $を作ります。shapeは(4, 84, 84)のようになります。これをニューラルネットワークへの入力とします。

状態s

ネットワークの構成

Q関数を近似するのに使う畳み込みニューラルネットワーク（CNN）の構造になります。

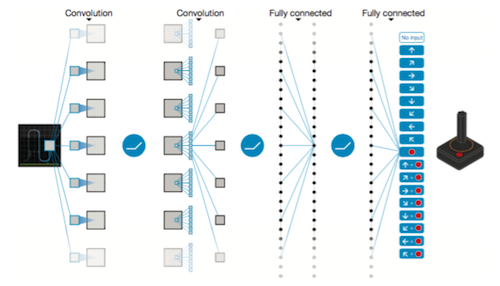
CNNの構造（Mnih et al., 2015）

状態$ s $を入力として、それぞれのゲーム操作$ a $の行動価値$ Q(s, a;\theta) $を出力します。出力層のユニット数はプレイするゲームのアクション数になります。

そして、それらのユニットの中から最大値を出力しているユニットを選ぶことで、最適行動$ \pi (s) = \text{argmax}_{a} Q(s, a;\theta) $を決定します。

CNNの各パラメータは以下のようになっています。

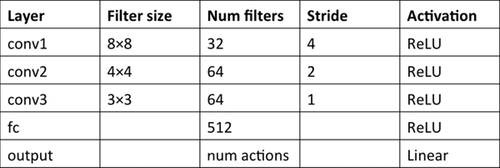
CNNの構成

報酬の固定

Atariはゲームによってスコアのレンジがまちまち（例えば+1や+20など）なので、報酬をある値に固定します。つまり、値の大きさにかかわらず、報酬が負だったら-1、正だったら1、0はそのままにします。これによって誤差微分の大きさを制限することができ、すべてのゲームで同じ学習率を使うことができるようになります（より汎用的になる）。

フレームスキップ

Atariでは1秒間に画面が60回更新されます。毎フレーム見るのは計算コストの面で効率的ではなく、実行時間を増やすことなくより多くのゲームをプレイさせるために、4フレームに一回見て行動選択をするようにします。スキップするフレームでは前回取った行動をリピートするようにします。

$ \epsilon $-greedy法

行動選択には$ \epsilon $-greedy法を使いますが、$ \epsilon $は1.0を初期値として、そこから0.1まで100万フレーム間で線形に減少させ、それ以降は0.1に固定します。

Experience Replay

Replay Memoryに一定の数だけ過去の遷移を保存して学習に使います。Mnih et al., 2015では100万遷移分を保存していますが、実験ではその量はメモリに載らないので、40万遷移分を保存します。なおその数を超えた分は古い遷移から消えていくようにします。

初期のReplay Memoryの確保

開始時は学習に使われるReplay Memoryが貯まっていないので、最初あるフレーム分ランダムに行動しReplay Memoryを蓄積させます。その間学習も行いません。Mnih et al., 2015では最初に5万遷移分貯めていますが、実験では2万遷移分にしました。

Target Network

教師信号$ r + \gamma \text{max} _{a’} \hat{Q}(s’, a’; \theta ^{-}) $のQ値を出力するためのTarget Networkを作り、1万フレームごとにTarget Networkの$ \theta ^{-} $にQ Networkの$ \theta $をコピーすることで更新します。

学習間隔

毎フレームで学習するのは計算量が多くなるだけなので、行動を4回行うごとに学習を行うようにします。

エラーのクリップ

学習の安定性を向上させるために、エラーである$ \text{target} - Q(s, a; \theta) $の値を-1から1の範囲でクリップします。-1よりも小さな値は-1、1よりも大きな値は1、-1と1の間の値はそのまま使用するという意味です。

このエラーのクリップは意外と重要なのですが、論文ではさらっとしか触れられていなかったり、説明が少し分かりにくいこともあって、間違って実装されてしまうことが多いようです。そのため、この部分はなるべく丁寧に説明します。

$ e \equiv \text{target} - Q(s, a; \theta) $とすると、損失関数は

$L = \frac{1}{2} \mathbb{E} \left[ e^2 \right]$

と書くことができます。この時点で$e$を[-1, 1]にクリップすると実は間違いです。なぜこれではいけないのでしょうか。[-1, 1]の外の値は全て-1または1に変換されてしまうので値が一定となり、そこでの勾配がゼロになってしまいます。[-1, 1]の範囲外の値を取るということはtargetとの差が大きいので、本来は勾配も大きくなるはずです。しかし、勾配がゼロになってしまうことにより学習がうまく進みません。

Mnih et al., 2015ではこちらの微分した式の方で$e$を[-1, 1]にクリップしています。

$\nabla L = \mathbb{E} \left[ e \nabla Q(s, a; \theta) \right]$

これは[-1, 1]の範囲の値に対しては上記の式がそのまま適用されますが、[-1, 1]の外の値に対しては

$\nabla L = \mathbb{E} \left[ \pm 1 \nabla Q(s, a; \theta) \right]$

という式を計算していることに相当します。この操作は一体何を意味するのでしょうか。微分である$ \nabla L $ではなく、もとの損失関数$ L $を考えてみます。積分すると、

$L = \mathbb{E} \left[ |e| \right]$

という式が得られます。まとめると、

$\begin{eqnarray} L =\left\{ \begin{array}{ll} \frac{1}{2} \mathbb{E} \left[ e^2 \right] & ([-1, 1]) \\ \mathbb{E} \left[ |e| \right] & (\text{outside of }[-1, 1]) \\ \end{array} \right. \end{eqnarray}$

となり、区間によって異なる損失関数を使っていることになります。$ e $が大きくなるに連れて$ e ^2 $の傾きはどんどん大きくなっていきますが、$ |e| $の傾きは$ \pm 1 $で一定です。つまり、$ |e| $は$ e ^2 $よりも鈍感に反応します。この性質を使って安定性を向上させていると考えることができます。

実装方法は2種類考えられます。一つは$ L $を明示的に定義せず、$ \nabla L $を定義してそこでクリップする方法です。もう一つは、いつも通り$ L $を明示的に定義する方法です。

Mnih et al., 2015では前者の方法で実装しているようですが、後者の方が分かりやすいかもしれません。後者の方法では$ L $は区間によって異なる関数形になっていますが、一本の式にまとめてしまうとよいと思います（交差エントロピーも元々は場合分けで表現されていましたが、損失関数として使う場合には一本の式にまとめられています。それに少し近いイメージでしょうか）。

エピソード開始時に「何もしない」フレーム

エピソード開始時の初期状態をランダムにするために、最大30フレームのランダムなフレーム数分「何もしない」行動を取り、画面を遷移させます。

実装

ではコードを見ながら解説していきます。なおここで使われるコードは断片的で省略してる箇所もあるので、全ソースコードはこちらから確認してみてください。

今回Atariのエミュレータを動かすために、OpenAI Gymを使いました。OpenAI Gymは、強化学習のための環境を簡単に構築できるオープンソースのライブラリです。具体的な詳細、インストール方法はGitHubかDocumentationを参照してください。

まずGymを使って大枠を書いてみます。

import gym

ENV_NAME = 'Breakout-v0'  # Gymの環境名
NUM_EPISODES = 12000  # プレイするエピソード数
NO_OP_STEPS = 30  # エピソード開始時に「何もしない」最大フレーム数

env = gym.make(ENV_NAME)  # Breakout-v0の環境を作る
agent = Agent(num_actions=env.action_space.n)  # Agentクラスのインスタンスを作る

for _ in xrange(NUM_EPISODES):
    terminal = False  # エピソード終了判定を初期化
    observation = env.reset()  # 環境の初期化、初期画面を返す
    for _ in xrange(random.randint(1, NO_OP_STEPS)):  # ランダムなフレーム数分「何もしない」行動で遷移させる
        last_observation = observation
        observation, _, _, _ = env.step(0)  # 「何もしない」行動を取り、次の画面を返す
    state = agent.get_initial_state(observation, last_observation)  # 初期状態を作る
    while not terminal:  # 1エピソードが終わるまでループ
        last_observation = observation
        action = agent.get_action(state)  # 行動を選択
        observation, reward, terminal, _ = env.step(action)  # 行動を実行して、次の画面、報酬、終了判定を返す
        env.render()  # 画面出力
        processed_observation = preprocess(observation, last_observation)  # 画面の前処理
        state = agent.run(state, action, reward, terminal, processed_observation)  # 学習を行う、次の状態を返す

分からない関数がいろいろ出てきてますが、基本的には環境とAgentクラスを用意して、先程あったDQNのアルゴリズムの流れに沿って組んでいきました。

具体的にそれぞれについて見ていきたいと思います。

Agentクラス

アルゴリズムのほとんどはAgentクラスに関数として実装しました。いくつかの関数は流れに沿ってあとから説明するとして、Agentクラスのインスタンスが作られたときに、どのように初期化されているかを見ていきたいと思います。

Agentクラスのinit()関数はこのようになっています。

import tensorflow as tf
from collections import deque

INITIAL_EPSILON = 1.0  # ε-greedy法のεの初期値
FINAL_EPSILON = 0.1  # ε-greedy法のεの終値
EXPLORATION_STEPS = 1000000  # ε-greedy法のεが減少していくフレーム数

class Agent():
    def __init__(self, num_actions):
        self.num_actions = num_actions  # 行動数
        self.epsilon = INITIAL_EPSILON  # ε-greedy法のεの初期化
        self.epsilon_step = (INITIAL_EPSILON - FINAL_EPSILON) / EXPLORATION_STEPS  # εの減少率
        self.time_step = 0  # タイムステップ
        self.repeated_action = 0  # フレームスキップ間にリピートする行動を保持するための変数

        # Replay Memoryの初期化
        self.replay_memory = deque()

        # Q Networkの構築
        self.s, self.q_values, q_network = self.build_network()
        q_network_weights = q_network.trainable_weights

        # Target Networkの構築
        self.st, self.target_q_values, target_network = self.build_network()
        target_network_weights = target_network.trainable_weights

        # 定期的にTarget Networkを更新するための処理の構築
        self.update_target_network = [target_network_weights[i].assign(q_network_weights[i]) for i in xrange(len(target_network_weights))]

        # 誤差関数や最適化のための処理の構築
        self.a, self.y, self.loss, self.grad_update = self.build_training_op(q_network_weights)

        # Sessionの構築
        self.sess = tf.InteractiveSession()

        # 変数の初期化（Q Networkの初期化）
        self.sess.run(tf.initialize_all_variables())

        # Target Networkの初期化
        self.sess.run(self.update_target_network)

ここで行われている主なことは、Replay Memoryの初期化、Q NetworkとTarget Networkの構築及び初期化、Target Network更新のための処理の構築、そして最適化のための処理の構築です。

Replay Memoryの初期化
Experience Replayで使われるReplay Memoryを保存しておく場所をdeque()で作ります。これで両端におけるappendやpopを高速に行えるリスト風のコンテナが作られます。
Q NetworkとTarget Networkの構築
2つのネットワークの構築には同じ関数を使います。build_network()関数は以下のようになっています。

import tensorflow as tf
from keras.models import Sequential
from keras.layers import Convolution2D, Flatten, Dense

STATE_LENGTH = 4  # 状態を構成するフレーム数
FRAME_WIDTH = 84  # リサイズ後のフレーム幅
FRAME_HEIGHT = 84  # リサイズ後のフレーム高さ

class Agent():
    .
    .
    .
    def build_network(self):
        model = Sequential()
        model.add(Convolution2D(32, 8, 8, subsample=(4, 4), activation='relu', input_shape=(STATE_LENGTH, FRAME_WIDTH, FRAME_HEIGHT)))
        model.add(Convolution2D(64, 4, 4, subsample=(2, 2), activation='relu'))
        model.add(Convolution2D(64, 3, 3, subsample=(1, 1), activation='relu'))
        model.add(Flatten())
        model.add(Dense(512, activation='relu'))
        model.add(Dense(self.num_actions))

        s = tf.placeholder(tf.float32, [None, STATE_LENGTH, FRAME_WIDTH, FRAME_HEIGHT])
        q_values = model(s)

        return s, q_values, model

ネットワークの構築はKerasとTensorFlowで書きました。TensorFlowだけで書くよりシンプルになっています。いっしょに使う場合の詳細はKerasのブログ記事をチェックしてみてください。

Target Network更新のための処理の構築
定期的にTarget NetworkにQ Networkの重みをコピーして更新します。

q_network_weights = q_network.trainable_weights
target_network_weights = target_network.trainable_weights
self.update_target_network = [target_network_weights[i].assign(q_network_weights[i]) for i in xrange(len(target_network_weights))]

Kerasのtrainable_weights関数で学習される重みのリストを取ってきてくれます。TensorFlowのassign()関数を使ってTarget Networkの重みにQ Networkの重みを代入する処理が書けます。これで定期的にself.sess.run(self.update_target_network)でTarget Networkを更新することができます。

最適化のための処理の構築
build_training_op()関数を見てみます。

import tensorflow as tf

LEARNING_RATE = 0.00025  # RMSPropで使われる学習率
MOMENTUM = 0.95  # RMSPropで使われるモメンタム
MIN_GRAD = 0.01  # RMSPropで使われる0で割るのを防ぐための値

class Agent():
    .
    .
    .
    def build_training_op(self, q_network_weights):
        a = tf.placeholder(tf.int64, [None])  # 行動
        y = tf.placeholder(tf.float32, [None])  # 教師信号

        a_one_hot = tf.one_hot(a, self.num_actions, 1.0, 0.0)  # 行動をone hot vectorに変換する
        q_value = tf.reduce_sum(tf.mul(self.q_values, a_one_hot), reduction_indices=1)  # 行動のQ値の計算

        # エラークリップ
        error = tf.abs(y - q_value)
        quadratic_part = tf.clip_by_value(error, 0.0, 1.0)
        linear_part = error - quadratic_part
        loss = tf.reduce_mean(0.5 * tf.square(quadratic_part) + linear_part)  # 誤差関数

        optimizer = tf.train.RMSPropOptimizer(LEARNING_RATE, momentum=MOMENTUM, epsilon=MIN_GRAD)  # 最適化手法を定義
        grad_update = optimizer.minimize(loss, var_list=q_network_weights)  # 誤差最小化

        return a, y, loss, grad_update

ここで、エラークリップを行っています。誤差関数は[-1, 1]内とその区間外で異なる関数形になっていて、それらを一本の式にまとめて定義しています。

OptimizerはMnih et al., 2015と同様にRMSPropを使っています。

誤差最小化を行う処理では、var_list=q_network_weightsを渡しています。これは、Q Networkの重みだけを最適化の対象にして、Target Networkの重みを誤って最適化してしまわないようにするためです。

ゲームプレイ部分

Agentクラスのインスタンスの初期化で何が行われているかについて見ました。
ではもう一度、大枠のコードに戻ってみましょう。

import gym

ENV_NAME = 'Breakout-v0'  # Gymの環境名
NUM_EPISODES = 12000  # プレイするエピソード数
NO_OP_STEPS = 30  # エピソード開始時に「何もしない」最大フレーム数

env = gym.make(ENV_NAME)  # Breakout-v0の環境を作る
agent = Agent(num_actions=env.action_space.n)  # Agentクラスのインスタンスを作る

for _ in xrange(NUM_EPISODES):
    terminal = False  # エピソード終了判定を初期化
    observation = env.reset()  # 環境の初期化、初期画面を返す
    for _ in xrange(random.randint(1, NO_OP_STEPS)):  # ランダムなフレーム数分「何もしない」行動で遷移させる
        last_observation = observation
        observation, _, _, _ = env.step(0)  # 「何もしない」行動を取り、次の画面を返す
    state = agent.get_initial_state(observation, last_observation)  # 初期状態を作る
    while not terminal:  # 1エピソードが終わるまでループ
        last_observation = observation
        action = agent.get_action(state)  # 行動を選択
        observation, reward, terminal, _ = env.step(action)  # 行動を実行して、次の画面、報酬、終了判定を返す
        env.render()  # 画面出力
        processed_observation = preprocess(observation, last_observation)  # 画面の前処理
        state = agent.run(state, action, reward, terminal, processed_observation)  # 学習を行う、次の状態を返す

前準備は整ったので、ゲームをプレイしていく部分に入っていきます。

エピソード開始時には主に以下の処理を行います。

env.reset()で環境を初期化する
初期状態をランダムにするために、最大30フレームのランダムなフレーム数分「何もしない」行動を取り、画面を遷移させる
get_initial_state()関数で初期状態を作る

get_initial_state()関数の中身を見てみましょう。

import numpy as np
from skimage.color import rgb2gray
from skimage.transform import resize

STATE_LENGTH = 4  # 状態を構成するフレーム数
FRAME_WIDTH = 84  # リサイズ後のフレーム幅
FRAME_HEIGHT = 84  # リサイズ後のフレーム高さ

class Agent():
    .
    .
    .
    def get_initial_state(self, observation, last_observation):
        processed_observation = np.maximum(observation, last_observation)
        processed_observation = np.uint8(resize(rgb2gray(processed_observation), (FRAME_WIDTH, FRAME_HEIGHT)) * 255)
        state = [processed_observation for _ in xrange(STATE_LENGTH)]
        return np.stack(state, axis=0)

ここではまず、現在のゲーム画面と前画面の各ピクセルごとに最大値を取っています。そのあと、グレースケール変換、リサイズを行い、最後に定められたフレーム数分だけスタックさせて初期状態を作っています。

ここで前処理された画面をuint8に変換している理由は、前処理後のフレームのデータ型がfloat64で、これは後に出てくるReplay Memoryに保存する際にメモリを圧迫し、保存できる遷移数が少なくなってしまうからです。

ちなみに画像の加工にはPythonの画像処理のライブラリであるscikit-imageを使っています。インストールがすごく簡単なので(pipでいける)、個人的にはOpenCVより好きです。

次に、各エピソード内で行う処理の流れについて説明します。

まずは、現在の状態での行動を選択します。行動選択はget_action()関数で行います。

import random
import numpy as np
import tensorflow as tf

ACTION_INTERVAL = 4  # フレームスキップ数
INITIAL_REPLAY_SIZE = 20000  # 学習前に事前に確保するReplay Memory数

class Agent():
    .
    .
    .
    def get_action(self, state):
        action = self.repeated_action  # 行動リピート

        if self.t % ACTION_INTERVAL == 0:
            if self.epsilon >= random.random() or self.t < INITIAL_REPLAY_SIZE:
                action = random.randrange(self.num_actions)  # ランダムに行動を選択
            else:
                action = np.argmax(self.q_values.eval(feed_dict={self.s: [np.float32(state / 255.0)]}))  # Q値が最も高い行動を選択
            self.repeated_action = action  # フレームスキップ間にリピートする行動を格納

        # εを線形に減少させる
        if self.epsilon > FINAL_EPSILON and self.t >= INITIAL_REPLAY_SIZE:
            self.epsilon -= self.epsilon_step

        return action

まず、フレームスキップがあるので、4フレームに一度行動を選択することになります。フレームがスキップされている間は、前に選択した行動をリピートするようにしています。

また、初期のReplay Memory数確保のために、最初のある一定のフレーム間はランダムな行動選択をすることになります。

行動選択は$ \epsilon $-greedy法に従います。確率$ \epsilon $でランダムに行動選択を行い、それ以外ではQ値が最も高い行動を選択することになります。

$ \epsilon $-greedy法の$ \epsilon $は1.0からある一定のフレーム間で線形に減少していき、やがて0.1に落ち着きます。

行動選択ができました。大枠のコードに戻ります。

import gym

ENV_NAME = 'Breakout-v0'  # Gymの環境名
NUM_EPISODES = 12000  # プレイするエピソード数
NO_OP_STEPS = 30  # エピソード開始時に「何もしない」最大フレーム数

env = gym.make(ENV_NAME)  # Breakout-v0の環境を作る
agent = Agent(num_actions=env.action_space.n)  # Agentクラスのインスタンスを作る

for _ in xrange(NUM_EPISODES):
    terminal = False  # エピソード終了判定を初期化
    observation = env.reset()  # 環境の初期化、初期画面を返す
    for _ in xrange(random.randint(1, NO_OP_STEPS)):  # ランダムなフレーム数分「何もしない」行動で遷移させる
        last_observation = observation
        observation, _, _, _ = env.step(0)  # 「何もしない」行動を取り、次の画面を返す
    state = agent.get_initial_state(observation, last_observation)  # 初期状態を作る
    while not terminal:  # 1エピソードが終わるまでループ
        last_observation = observation
        action = agent.get_action(state)  # 行動を選択
        observation, reward, terminal, _ = env.step(action)  # 行動を実行して、次の画面、報酬、終了判定を返す
        env.render()  # 画面出力
        processed_observation = preprocess(observation, last_observation)  # 画面の前処理
        state = agent.run(state, action, reward, terminal, processed_observation)  # 学習を行う、次の状態を返す

行動を選択したら、env.step(action)で行動を実行することで、画面が遷移し、次の画面、報酬、終了判定を受け取ります。

続いて、受け取った画面をpreprocess()関数で前処理にかけます。

import numpy as np
from skimage.color import rgb2gray
from skimage.transform import resize

FRAME_WIDTH = 84  # リサイズ後のフレーム幅
FRAME_HEIGHT = 84  # リサイズ後のフレーム高さ

def preprocess(observation, last_observation):
    processed_observation = np.maximum(observation, last_observation)
    processed_observation = np.uint8(resize(rgb2gray(processed_observation), (FRAME_WIDTH, FRAME_HEIGHT)) * 255)
    return np.reshape(processed_observation, (1, FRAME_WIDTH, FRAME_HEIGHT))

現在の画面と前の画面の各ピクセルにおいて最大値を取り、そのあとグレースケール変換、リサイズを行います。ここでも先程と同じく、前処理された画面をuint8に変換しています。最後にnp.reshape()で扱いやすいようにshapeを整えています（CNNに入力できるshapeにしている）。

ここまでで状態、行動、報酬、終了判定、新たに観測した画面が揃いました。これをrun()関数に投げて、中では学習が行われることになります。そして最終的には次の状態が返ってくることになります。アルゴリズムでいうとクライマックスである学習のパートをこれから説明します。

import numpy as np
import tensorflow

NUM_REPLAY_MEMORY = 400000  # Replay Memory数
INITIAL_REPLAY_SIZE = 20000  # 学習前に事前に確保するReplay Memory数
TRAIN_INTERVAL = 4  # 学習を行う間隔
TARGET_UPDATE_INTERVAL = 10000  # Target Networkの更新をする間隔

class Agent():
    .
    .
    .
    def run(self, state, action, reward, terminal, observation):
        # 次の状態を作成
        next_state = np.append(state[1:, :, :], observation, axis=0)

        # 報酬の固定、正は1、負は-1、0はそのまま
        reward = np.sign(reward)

        # Replay Memoryに遷移を保存
        self.replay_memory.append((state, action, reward, next_state, terminal))
        # Replay Memoryが一定数を超えたら、古い遷移から削除
        if len(self.replay_memory) > NUM_REPLAY_MEMORY:
            self.replay_memory.popleft()

        if self.t > INITIAL_REPLAY_SIZE:
            # Q Networkの学習
            if self.t % TRAIN_INTERVAL == 0:
                self.train_network()

            # Target Networkの更新
            if self.t % TARGET_UPDATE_INTERVAL == 0:
                self.sess.run(self.update_target_network)

        self.t += 1  # タイムステップ

        return next_state

まず、現在の状態と観測した画面を使って次の状態を作ります。

ここで、報酬の固定も行っておきます。

$ (s, a, r, s’, terminal) $として、Replay Memoryに遷移を保存します。Replay Memoryは一定数を超えたら古い遷移から削除していきます。

Q Networkの学習は、Replay Memory数を確保しているフレーム間では行われません。また、4フレーム（4回行動する）ごとに学習が行われるようにしています。train_network()関数で学習を行います。

Target Networkは1万フレームごとに更新を行います。

それではtrain_network()関数を見てみましょう。

import random
import numpy as np
import tensorflow as tf

BATCH_SIZE = 32  # バッチサイズ
GAMMA = 0.99  # 割引率

class Agent():
    .
    .
    .
    def train_network(self):
        state_batch = []
        action_batch = []
        reward_batch = []
        next_state_batch = []
        terminal_batch = []
        y_batch = []

        # Replay Memoryからランダムにミニバッチをサンプル
        minibatch = random.sample(self.replay_memory, BATCH_SIZE)
        for data in minibatch:
            state_batch.append(data[0])
            action_batch.append(data[1])
            reward_batch.append(data[2])
            next_state_batch.append(data[3])
            terminal_batch.append(data[4])

        # 終了判定をTrueは1に、Falseは0に変換
        terminal_batch = np.array(terminal_batch) + 0

        target_q_values_batch = self.target_q_values.eval(feed_dict={self.st: np.float32(np.array(next_state_batch) / 255.0)})  # Target Networkで次の状態でのQ値を計算
        y_batch = reward_batch + (1 - terminal_batch) * GAMMA * np.max(target_q_values_batch, axis=1)  # 教師信号を計算

        # 勾配法による誤差最小化
        loss, _ = self.sess.run([self.loss, self.grad_update], feed_dict={
            self.s: np.float32(np.array(state_batch) / 255.0),
            self.a: action_batch,
            self.y: y_batch
        })

ここではReplay Memoryに保存された遷移をランダムサンプリングし、それをミニバッチとして学習に使います。

またTarget Networkを使って次の状態のQ値を計算し、それを使って教師信号を計算しています。

最後にミニバッチでの勾配法による誤差最小化を行っています。

大枠のコードを再掲します。

import gym

ENV_NAME = 'Breakout-v0'  # Gymの環境名
NUM_EPISODES = 12000  # プレイするエピソード数
NO_OP_STEPS = 30  # エピソード開始時に「何もしない」最大フレーム数

env = gym.make(ENV_NAME)  # Breakout-v0の環境を作る
agent = Agent(num_actions=env.action_space.n)  # Agentクラスのインスタンスを作る

for _ in xrange(NUM_EPISODES):
    terminal = False  # エピソード終了判定を初期化
    observation = env.reset()  # 環境の初期化、初期画面を返す
    for _ in xrange(random.randint(1, NO_OP_STEPS)):  # ランダムなフレーム数分「何もしない」行動で遷移させる
        last_observation = observation
        observation, _, _, _ = env.step(0)  # 「何もしない」行動を取り、次の画面を返す
    state = agent.get_initial_state(observation, last_observation)  # 初期状態を作る
    while not terminal:  # 1エピソードが終わるまでループ
        last_observation = observation
        action = agent.get_action(state)  # 行動を選択
        observation, reward, terminal, _ = env.step(action)  # 行動を実行して、次の画面、報酬、終了判定を返す
        env.render()  # 画面出力
        processed_observation = preprocess(observation, last_observation)  # 画面の前処理
        state = agent.run(state, action, reward, terminal, processed_observation)  # 学習を行う、次の状態を返す

これで一巡することができました。run()関数によって返ってきた次の状態は現在の状態となり、今までの操作を終了判定が出るまで繰り返します。そしてそれを定めたエピソード数分だけ繰り返します。

これでDQNのアルゴリズムを一通り実装することができました。

実験

というわけで実際に動かしてみましょう。ちなみに、今回はブロック崩しを例に実験してみましたが、コードのENV_NAMEのGymの環境名を変えれば、基本的にはAtariのどのゲームでもプレイさせることができます。

お手元のPCで動かしてみる

必要なものをインストールします。

gym（Atari環境）
scikit-image
keras
tensorflow

GitHubから今回のコードをcloneしてきて実行してください。

$ git clone https://github.com/elix-tech/dqn
$ cd dqn
$ python dqn.py

CPU上での学習はすごく時間がかかってしまうので大変ですが、学習済み（とは言っても1日とちょっとしかしていませんが）の重みを提供しているので、是非それを使ってテストモードでDQNにゲームをプレイさせてみてください。学習済みの重みはリポジトリに入っています。

GPUで動かしてみる

今回の実験はGPU上で行いました。AWS EC2のg2.2xlargeでスポットインスタンスを使いました。

今回の実験に伴ってコードが動く環境をAWS上に構築したので、AMIとして提供しています。是非それを使ってGPUでも動かしてみてください。

AMIはDQN-AMIという名前で、AMI IDはami-487cb85eです。リージョンはN. Virginiaです。Ubuntu上にTensorFlow, Keras, scikit-image, OpenAI Gym, CUDA, cuDNNがプリインストールしてあります。コードはscpで転送するか、インスタンス上でgit cloneをして取ってきてください。

また、GPU上ではGymのenv.render()で画面を出力できるようにしていないので、動かす際はコメントアウトするか、Gymのリポジトリに書いてある必要なものをインストールしてください（おそらく画面を出力しない方が速いのではないかと思い出力しませんでしたが実際どうなんでしょう）。

結果

DQNにブロック崩しをプレイさせてみました。AWS上で合計約28時間の学習（1万2千エピソード、470万フレーム）を行いました。

テストプレイ

まだそこまでうまくプレイはできていないですね。学習途中の子供のようです。ですがもっと学習すればもっとパフォーマンスが上がるはずです。

グラフ結果

エピソードあたりの平均ロス、平均最大Q値、持続時間、合計報酬をTensorBoardで出力してみました。

まとめ

今回は少し時代遅れではありましたが、DQNのおさらい、そしてDQNをMnih et al., 2015を参考に実装してみました。まだまだ改善の余地はありますが、今回はシンプルさを心がけました。みなさん自身が実際にコードを動かしてみてどんどん改善していってもらえればうれしいです。

強化学習、DQNは日々進化していて、Mnih et al., 2015が出たあとも、ものすごい勢いで論文が出続けています。下記はほんの一部です。

強化学習関連の論文をまとめてくれているありがたいリポジトリもGitHubにありました。

junhyukoh/deep-reinforcement-learning-papers

これを見るだけでも、強化学習だけで相当な量の論文があることが分かります。

またおもしろいテーマがあれば、是非記事にしてみなさんに共有できればと思っています。コメント、アドバイス、または動かしてみてこんな結果になったよ等、何でもどしどしお待ちしています。

参考文献

理論面

実装面