今回はadversarial exampleについて解説していきます。Adversarial exampleというのは、下図のように摂動を与えることによりモデルに間違った答えを出力させてしまうもののことです。



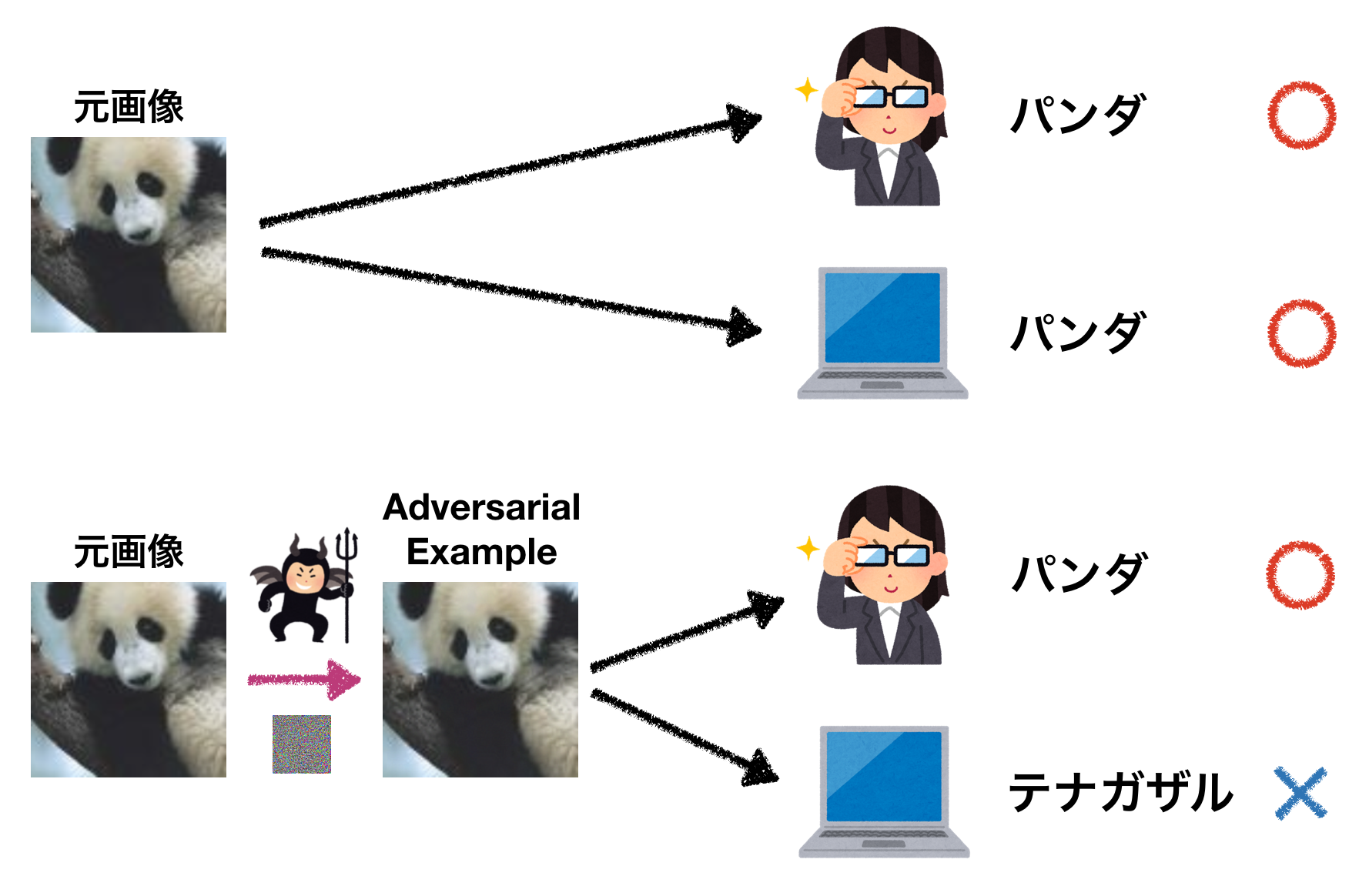
この例では、もともとモデルがパンダと正しく分類することができていた画像に摂動を与えることで、テナガザルと誤分類させています。しかし、人間には元の画像との違いはほとんど分からず、パンダのままに見えます。

Adversarial exampleは機械学習モデルを実用化していく上で大きな問題となります。例えば、交通標識をadversarial exampleにしてしまえば、自動運転車をだませてしまう可能性があります。

注目を集めてきている研究分野ですが、まだちゃんと調べたことがないという人も多いかと思います。今回もなるべく丁寧に解説していきたいと思います。


目次


基礎



Szegedy et al. (2013)

摂動を与えることにより誤分類してしまうというニューラルネットワークにおけるこのような性質はSzegedy et al. (2013)によって指摘され、adversarial exampleという名前が付けられています。


Source: Szegedy et al. (2013)


まずはこちらの図から見ていきましょう。左側の列は元画像です。これら元画像はAlextNetで正しいクラスに分類されています。これらの画像に摂動を与えた右側の列の画像は全て「ダチョウ」として間違って分類されてしまっています。摂動はランダムなノイズではなく、ある手法によって計算されたものです。

どのような方法でこのような画像を作ることができるでしょうか。勾配を使って簡単に作成することができます。ニューラルネットワークに学習させる時は通常重み \(\boldsymbol{w}\) を勾配降下法で更新し、入力 \(\boldsymbol{x}\) は固定していました。今回は逆に重み \(\boldsymbol{w}\) を固定し、入力 \(\boldsymbol{x}\) を変化させます。入力 \(\boldsymbol{x}\) に対する勾配を見ることで、入力をどのように変化させていけばダチョウというクラスに分類されるかが分かります。

このような手法で元画像を変化させていくと、どんな風に画像が変化していくでしょうか。例えば車の画像であれば、ダチョウクラスに向かって変化させていくと車の画像が徐々にダチョウっぽく変化していくと予想する人が多いのではないでしょうか。

実際にはそうはなりません。図のように人間には分からないレベルで僅かに変化するだけです。人間には元画像と全く同じように見えますが、モデルは高い確信度でダチョウだと分類するようになってしまいます。

実際には論文ではBox-constraind L-BFGSという手法を使っていて、下記の条件下で問題を解いています。

ここで \(\tilde{\boldsymbol{x}}\) は変化した入力、 \(l\) はターゲットのラベル、 \(n\) は次元数を表します。 狙ったターゲット \(l \) に向かって損失を最小化すると同時に \(\lVert \boldsymbol{x} - \tilde{\boldsymbol{x}} \rVert_2^2\) も最小化し、元画像との違いがなるべく小さくなるようにします。\(c > 0\)となる定数はLine searchにより \(\lVert \boldsymbol{x} - \tilde{\boldsymbol{x}} \rVert_2^2\) が最小となるように決めます。つまり、様々な値の \(c\) に対して上記の問題を解き、 \(\lVert \boldsymbol{x} - \tilde{\boldsymbol{x}} \rVert_2^2\) が最小となるadversarial exampleを探します。

Szegedy et al. (2013)では他にも次のような興味深いことが報告されています。

  • あるモデルのadversarial exampleは、異なるアーキテクチャのモデルでもよく誤分類される
  • あるデータで学習したモデルのadversarial exampleは、異なるデータ（training dataの異なるサブセット）で学習したモデルでもよく誤分類される
  • 線形分類器もadversarial exampleに対して脆弱

Adversarial exampleは他のモデルでも誤分類されてしまうことがよくあるということで、非常に興味深い結果です。

特定のモデルや特定のデータセットでのoverfittingがadversarial exampleの原因ではないかと考える人が多いのではないでしょうか。しかし、この結果を見るとどうもoverfittingや非線形性では説明がつかなそうです。


Goodfellow et al. (2014)

線形性による説明

Adversarial exampleはoverfittingや非線形性では説明がつかなそうだということが分かりました。それでは一体何が原因なのでしょうか。Goodfellow et al. (2014)では高次元空間での線形性で説明できるとしています。詳しく見ていきましょう。

元の入力を \(\boldsymbol{x}\) 、摂動を \(\boldsymbol{\eta}\) とすると、摂動を加えられた入力 \(\tilde{\boldsymbol{x}}\) は \(\tilde{\boldsymbol{x}} = \boldsymbol{x} + \boldsymbol{\eta}\) と表されます。ここでは小さな摂動を考えるため、小さな値\(\epsilon\)を用いて\( \lVert\boldsymbol{\eta}\rVert_\infty < \epsilon \)とします（\(\boldsymbol{\eta}\)の要素のうち一番大きなものでも\(\epsilon\)より小さいという意味です。画像のピクセルごとに摂動を与える時に、どれも\(\epsilon\)よりも小さい摂動を与えることになります）。

重み \(\boldsymbol{w}\) との内積は

と表されます。こうしてみるとアクティベーションは \(\boldsymbol{w}^\mathrm{T} \boldsymbol{\eta}\) とともに大きくなっていくことが分かります。ではどのような摂動 \(\boldsymbol{\eta}\) を与えればアクティベーションを大きくできるでしょうか。 \(\text{sign}(\boldsymbol{w})\) の方向に摂動を与えれば良さそうです。

なぜこの方向が良いのか簡単な例を使ってみてみます。

import numpy as np

w = np.array([-0.4, 0.5, -0.2, 0.4, -0.3, 0.6, -0.4, 0.1, -0.9, 0.7])
n = np.array([-1.0, -1.0, -1.0, 1.0, 1.0, -1.0, -1.0, 1.0, -1.0, -1.0]) # Random
e = np.sign(w)

print('e:', e)
print('w dot n:', np.dot(w, n))
print('w dot e:', np.dot(w, e))

# Results
# e: [-1.  1. -1.  1. -1.  1. -1.  1. -1.  1.]
# w dot n: 0.3
# w dot e: 4.5

適当な値の重み w を考えます。 n は -1と+1をランダムに与えたものです。これらの内積を取るとプラスとマイナスがおおよそ打ち消し合って 0.3 とゼロに近い値になりました。次に w と e の内積ついて考えてみます。 w の要素とそれに対応する e の要素は同じ符号を持つため、プラスの値が蓄積していき 4.5 という大きな値になっています（ \(\boldsymbol{w}^\mathrm{T} \text{sign}(\boldsymbol{w}) = \lVert \boldsymbol{w} \rVert_1 \) です）。ランダムなノイズではなく、特定の向きに摂動を与えることが重要であることも分かります。また、これは10次元の場合の例ですが、実際に扱われる画像の次元は遥かに大きいです。次元が大きくなればこの値もずっと大きくなります。

内積の式に戻って考えてみましょう。 \(\boldsymbol{w}\) の次元数を \(n\) 、要素の大きさの平均を \(m\) とします。そうするとアクティベーションは \(\epsilon m n\) に従って大きくなります。次元数 \(n\) が大きいほど摂動がアクティベーションに与える影響が大きくなります。摂動によるアクティベーションが大きくなると間違ったクラスに分類されてしまう可能性が高くなります。

\( \lVert\boldsymbol{\eta}\rVert_\infty \) は次元とともに大きくなっていくわけではありません。ピクセルごとにほんの僅かな変化があるだけです。アクティベーションが大きく変わるにも関わらず、人間には画像の変化はほとんど分からないことになります。

以上の議論を踏まえると、単純な線形モデルもadversarial exampleの影響を受けることになります。線形性が原因だとすれば、Szegedy et al. (2013)で浅いネットワークもadversarial exampleに対して脆弱だったことの説明もつきます。


Fast Gradient Sign Method (FGSM)

Goodfellow et al. (2014)では線形性に着目してFast Gradient Sign Method (FGSM) というadversarial exampleを高速に計算する手法を提案しています。ニューラルネットワークは非線形なのでは、と思うかもしれませんが、例えばReLUは意図的に線形性な振る舞いをするようにデザインされています。Sigmoidだとしてもなるべく勾配消失が起きないように線形性な部分を使うようにチューニングされていたりします。

それではどのような摂動を与えるのか式で見てみましょう。

\(y\) は \(\boldsymbol{x}\) に対応するラベルです。損失を最大化する方向に入力 \(\boldsymbol{x}\) を変化させるという意味の式になっています。正しいクラスに対する損失を増加させているだけなので、どのクラスに誤分類されるかは分かりません。また、 \(\nabla_\boldsymbol{x} (\boldsymbol{w}^\mathrm{T} \boldsymbol{x}) = \boldsymbol{w}\) なので、前のセクションで議論したのと同じような形になっています。これはイテレートするような手法ではなく、誤差逆伝播により一度勾配を計算するだけなので高速です。 \(\epsilon\) は固定された小さな値です。

このようにして作成されたのが下図です。よく引用される図なので見たことがある人も多いかもしれません。


Source: Goodfellow et al. (2014)


Szegedy et al. (2013)のBox-constraind L-BFGSを使った手法では、摂動が最小となるadversarial exampleを探すように設計されていますが、FGSMはより速く計算することを重視して設計されています。また、摂動の大きさを \(L_2\) と \(L_\infty\) で測っているという違いもあります。

FGSMに限った話ではありませんが、このような手法で作成した画像で必ずモデルに誤分類させられることが保証されているわけではありません。しかし、論文ではFGSMにより、多くのモデルでうまくadversarial exampleを見つけることができたと報告されています。単純なモデルであるlogistic regressionでもadversarial exampleを作ることができます。


Source: Goodfellow et al. (2014)


上図が実験結果です。この実験ではlogistic regressionを使ってMNISTの「3」と「7」に分類しています。元々はエラー率1.6%で3と7に分類できていましたが、FGSMにより生成されたadversarial exampleではエラー率が99%になってしまっています。

Linear classifierでのadversarial exampleについてはAndrej Karpathyのブログも分かりやすくおすすめです。


Adversarial Training

Adversarial exampleはディープラーニング特有の問題だと誤解されている場合がありますが、そうではありません。線形性に原因があることを考えるとlogistic regressionのような単純なモデルでも問題になります。

Universal approximator theoremは、中間層が1層以上で十分なユニットを持つニューラルネットワークはどんな関数でも表現しうることを保証しています。これを踏まえると、ニューラルネットワークはむしろadversarial exampleに対抗し得るポテンシャルがあることが分かります。（そのような関数が存在するとしても、学習によってそのような関数にたどり着けるかどうかは別問題です。）

Adversarial exampleに対する防御方法の一つとして、下記のようにadversarial exampleもtraining setに含めて学習するという方法が考えられます。

普通に学習するとadversarial exampleに対しエラー率が89.4%だったモデルで、上記のようにしてadversarial trainingを行うとエラー率が17.9%に下がったと報告されています。だいぶエラー率が下がりましたが、まだ2割近くもエラーがあります。また、FGSMによる攻撃はある程度防御できても、他の手法による攻撃には脆弱であると考えられます。このように様々な攻撃に対して有効な防御方法は少なくとも現時点では存在せず、更なる研究が求められています。


攻撃


ここまでFGSMなどの攻撃手法を見てきました。ここでは他の攻撃手法や異なる状況設定での攻撃について見ていきます。


Jacobian-Based Saliency Map Approach (JSMA)

JSMAはsource-target misclassificationと呼ばれるタイプの攻撃です。FGSMは何らかのクラスに誤分類させるという形でしたが、JSMAは特定の入力を特定の狙ったクラスに誤分類させます。下図を見ると分かりやすいと思います。これはMNISTを使った例で、特定の入力画像を狙った数字へと誤分類させています。


Source: Papernot et al. (2015b)


JSMAでは下記のように定義されるadversarial saliency mapを利用します。

\( \boldsymbol{X} \) は入力、\( \boldsymbol{F}_j \) はクラスjである確率（ニューラルネットワークの出力）、\(t\) はターゲット、\(i\) は入力の \(i\) 番目の特徴（例えば \(i\) 番目のピクセル）であることを表します。

ターゲット \(t\) に誤分類させるためには、\(t \neq j \) である \( \boldsymbol{F}_j \) を小さくしつつ、\( \boldsymbol{F}_t \) を大きくしてやれば良いと考えられます。そのためには、上記の \(S(\boldsymbol{X}, t)\) の値の大きな部分に対して \( \boldsymbol{X} \) を変化させてやれば良さそうです。ターゲット \(t\) に誤分類されるか、摂動の大きさが上限に達するまで繰り返して変化させていきます。

FGSMは多くのピクセルに少しずつ摂動を与えますが、JSMAは少数のピクセルにだけ摂動を与えて誤分類させるようになっています。また、JSMAはFGSMよりも計算コストがかかるという違いもあります。


Black-Box Attack

これまで見てきた攻撃方法は基本的にモデルやtraining setに直接アクセスできることが前提（white box）となっていました。しかし、APIを通じてモデルにアクセスする場合などを考えると、このような前提は現実的ではありません。ここでは、モデルのアーキテクチャやパラメータ、training setに関する情報がない状況での攻撃であるblack-box attackについて説明します。

基本的に利用できるのは、攻撃対象となるモデル（oracle）から得られるラベルだけです。このような状況でどのようにしてadversarial exampleを生成することができるでしょうか。

Papernot et al. (2016a)では、手元で代わりのモデル（substitute）に学習させ、そのモデルを使ってadversarial exampleを生成しています。このadversarial exampleはoracleをだませてしまう可能性が十分あります。なぜならこれまで見てきたように、あるモデルで生成したadversarial exampleは、他のモデルをもだますということがよく起きるからです。これがblack-box attackの大まかな仕組みです。

もう少し詳しく流れを見ていきましょう。Oracleが学習に使用したtraining setは分からないという前提なので、自分でtraining setを用意します。例えば、数字を認識するタスクであればMNISTっぽいデータセットを自分で用意します（ラベルは必要ありません）。Substituteのアーキテクチャも決めます。Oracleが画像分類を行っているのであれば、それっぽいCNNにしておこうかという感じで決めます（画像分類といえばCNNなので）。

次に、用意したデータセットに対してoracleでラベル付けを行います。例えばMNISTの場合、training setは6万枚の画像で構成されていますが、これと同程度の量のデータセットに対してラベル付けを行おうとするとかなり頻繁にAPIを呼び出すことになります。頻繁にAPIを呼び出すと運営側に攻撃を検知されやすくなってしまうため、100枚など少ないデータを用意します。


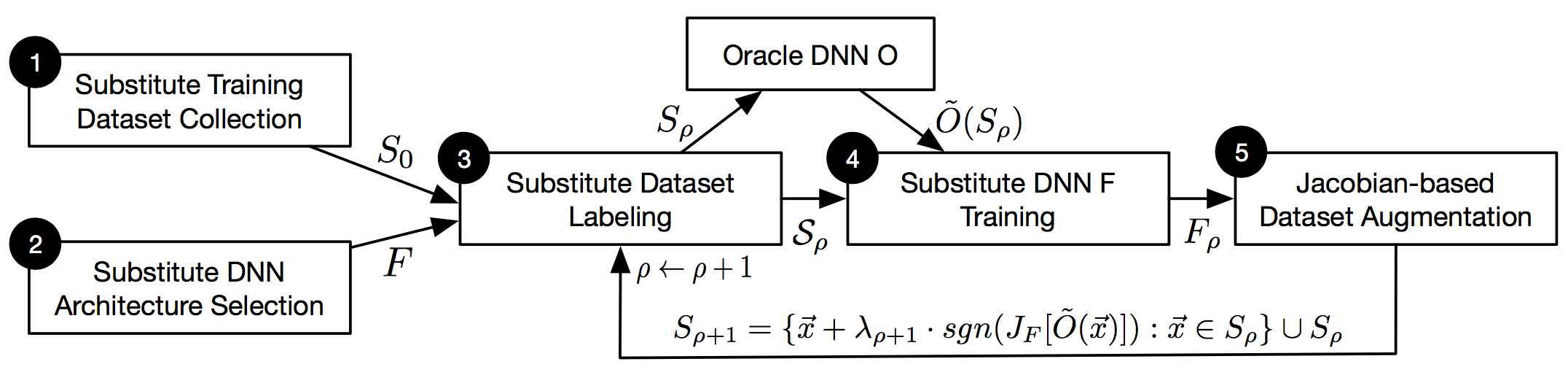
Source: Papernot et al. (2016a)


Substituteがoracleのdecision boundaryを学習しやすくするために、Jacobian-based data augmentationという手法を使ってデータを水増しします。上図中の式のようにJacobianを使って画像を僅かに変化させます。上図の3〜5のステップを繰り返し、学習が完了したらそのsubstituteを使ってFGSMなどの手法でadversarial exampleを生成することができます。

Papernot et al. (2016a)では上記の手法でMetaMind、Amazon、Googleが提供するAPIに実際に誤分類させることに成功しています。

Oracleやsubstituteはニューラルネットワークである必要はなく、他の機械学習手法にも適用できます。Papernot et al. (2016b)では異なるモデル間でのtransferabilityについて詳しく調べています。


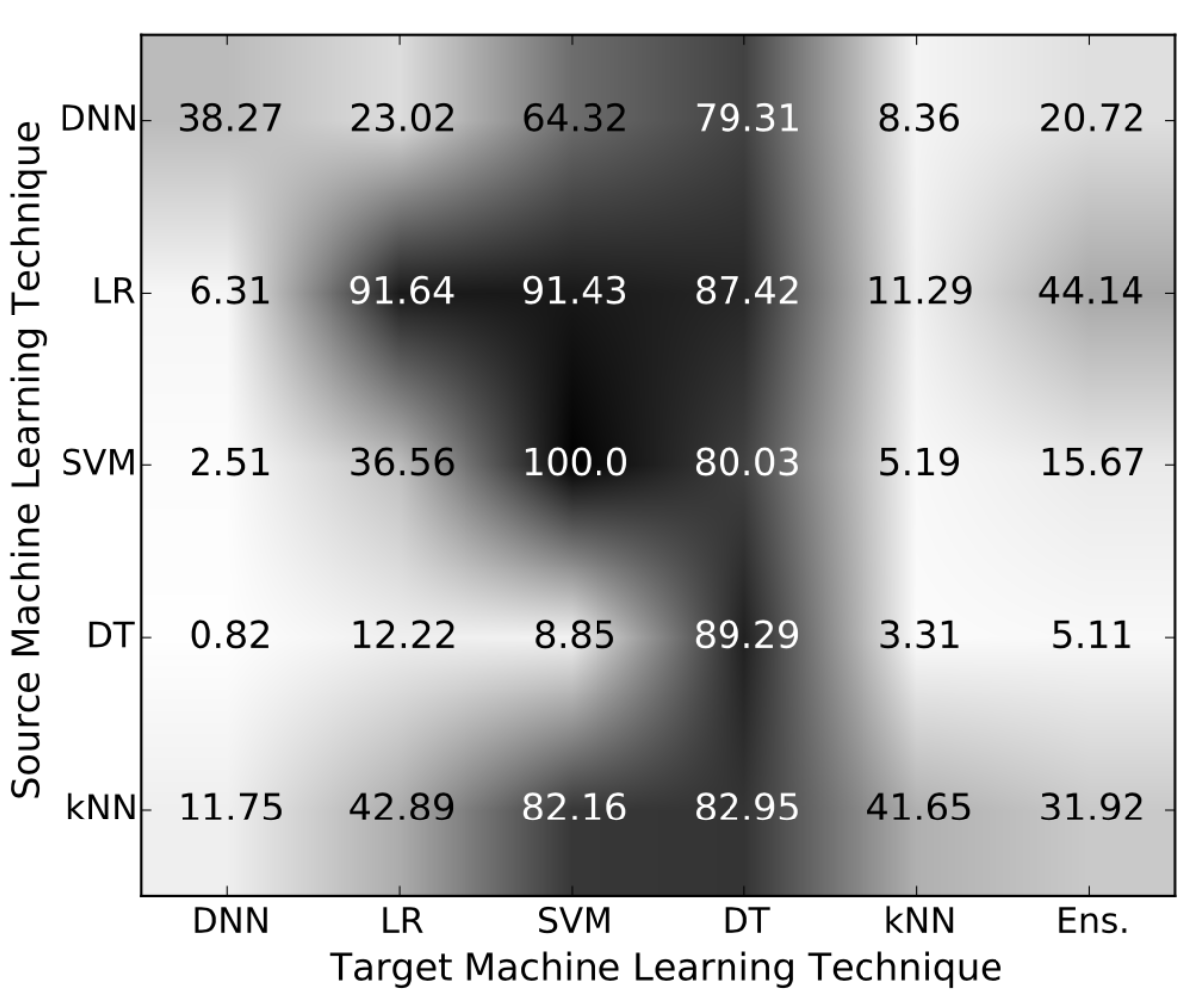
Source: Papernot et al. (2016b)


図中のSourceは、記載されている機械学習手法を使ってadversarial exampleを作成したことを意味します。Targetの方と合わせてみると、そのadversarial exampleがあるtargetで誤分類された割合が分かります。図中のEns.はDNN、LR、SVM、DT、kNNのアンサンブルのことです。

DT (Decision Tree)が一番脆弱であるという結果になっています。面白いことにアンサンブルも脆弱です。この中ではDNN (Deep Neural Network)が一番強いことが分かります。


防御


Defensive Distillation

Defensive distillationはPapernot et al. (2015a)によって提案されました。これは名前の通りdistillation（Hinton et al. 2015）という既存手法に基づく防御方法です。まずは簡単にdistillationについて説明します。

精度を上げるために巨大なニューラルネットワークを用いたり、アンサンブルにしたりといったことがありますが、そうするとデプロイが困難になってしまうという問題が生じます。特にスマートフォン上で動かしたりといったことを考えると、なるべく精度を保ちつつも、小さなネットワークにしたいという場合があります。Distillationはこのような場合に役に立ちます。

ここでは元の大きなネットワークを教師ネットワーク、新たな小さなネットワークを生徒ネットワークと呼ぶことにします。教師ネットワークはいつも通り [0, 1, 0,...] のようなラベル（hard target）を使って学習します。生徒ネットワークは、 [0.02, 0.96, 0.01, ...] というような教師ネットワークの出力（soft target）を使います。そして、生徒ネットワークは教師ネットワークと同じ出力になるように学習していきます。

教師ネットワークは正解となるクラス以外にも確率を割り振っています。これらの確率は、どのクラスとどのクラスが似ているといった情報を含んでいます。例えば乗用車とゴミ収集車は少しだけ似ていて間違える可能性はわずかにあっても、にんじんと間違える可能性はほとんどないことが分かったりします。

教師ネットワークの出力（soft target）にはこのような情報も含まれているため、生徒ネットワークはよりうまく学習することができそうです。また、soft targetにはregularizerとしての効果があることも分かっています。

実はこれだけでは生徒ネットワークはうまく学習できず、もう少し工夫が必要です。単純にsoft targetを使おうとしても、はずれのクラスに割り振られている確率は\(10^{-6}\)や\(10^{-9}\)のように非常に小さいためうまくいきません。そこで少し工夫して下記のようにsoftmaxで温度 \(T\) を考慮します。

\(T = 1\)の場合は通常のsoftmaxと同じです。\(T\) を大きくしていくと、はずれのクラスにもより大きな確率が割り振られるようになります。\(T \rightarrow \infty\) とすると、どのクラスに割り振られる確率も \(1/N\) と同じになります。

まとめると下図のような流れになります。 \(T\) を大きくしておくのは学習時のみで、テスト時は \(T = 1\) に戻します。


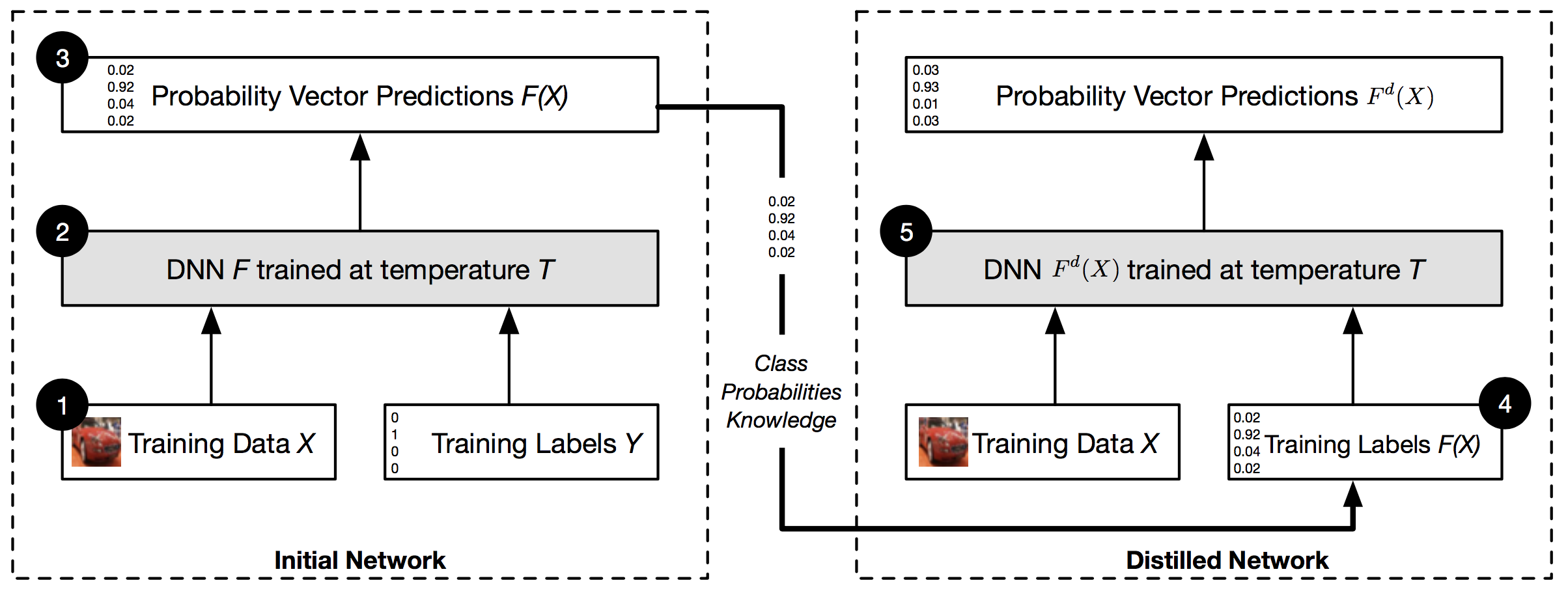
Source: Papernot et al. (2015a)


Defensive distillationでは、adversarial exampleによる攻撃を防ぐ目的でdistillationを使います。ネットワークを小さくすることが目的ではないため、Papernot et al. (2015a)では教師ネットワークと生徒ネットワークのアーキテクチャは同じにしてあります。

それでは実験結果を見てみましょう。


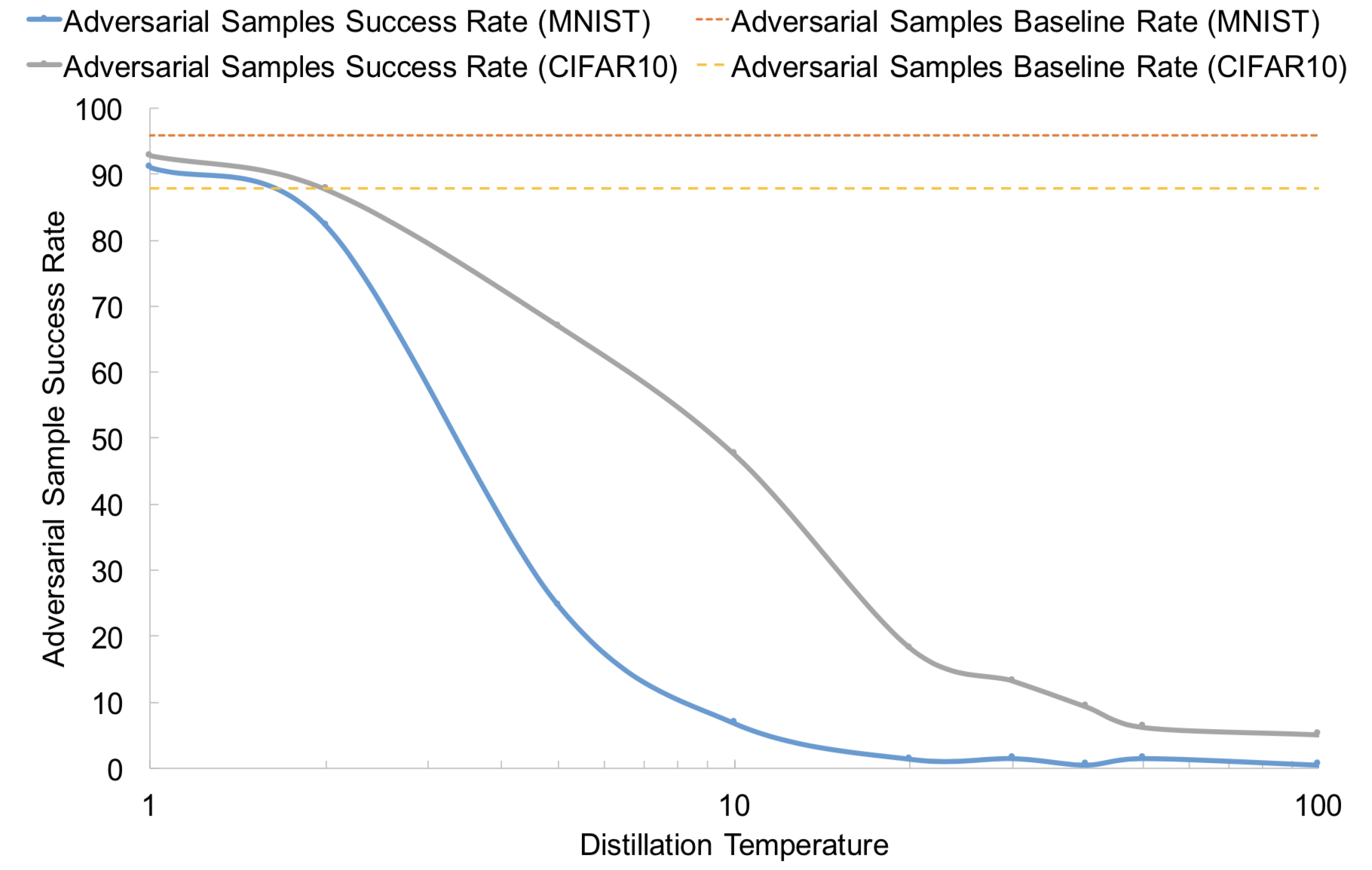
Source: Papernot et al. (2015a)


MNISTとCIFAR-10で実験を行っていて、上図はadversarial exampleによる攻撃の成功率を表しています。攻撃方法はJSMAです。温度が上昇するに連れて、成功率が下がっている様子が分かります。

温度を上げることで精度に影響が出ていないかも重要です。いくら防御できたとしてもあまりにもモデルの精度が下がってしまうと使い物にならなくなってしまうからです。下図を見ると精度にそれほど大きな影響はないことが分かります。


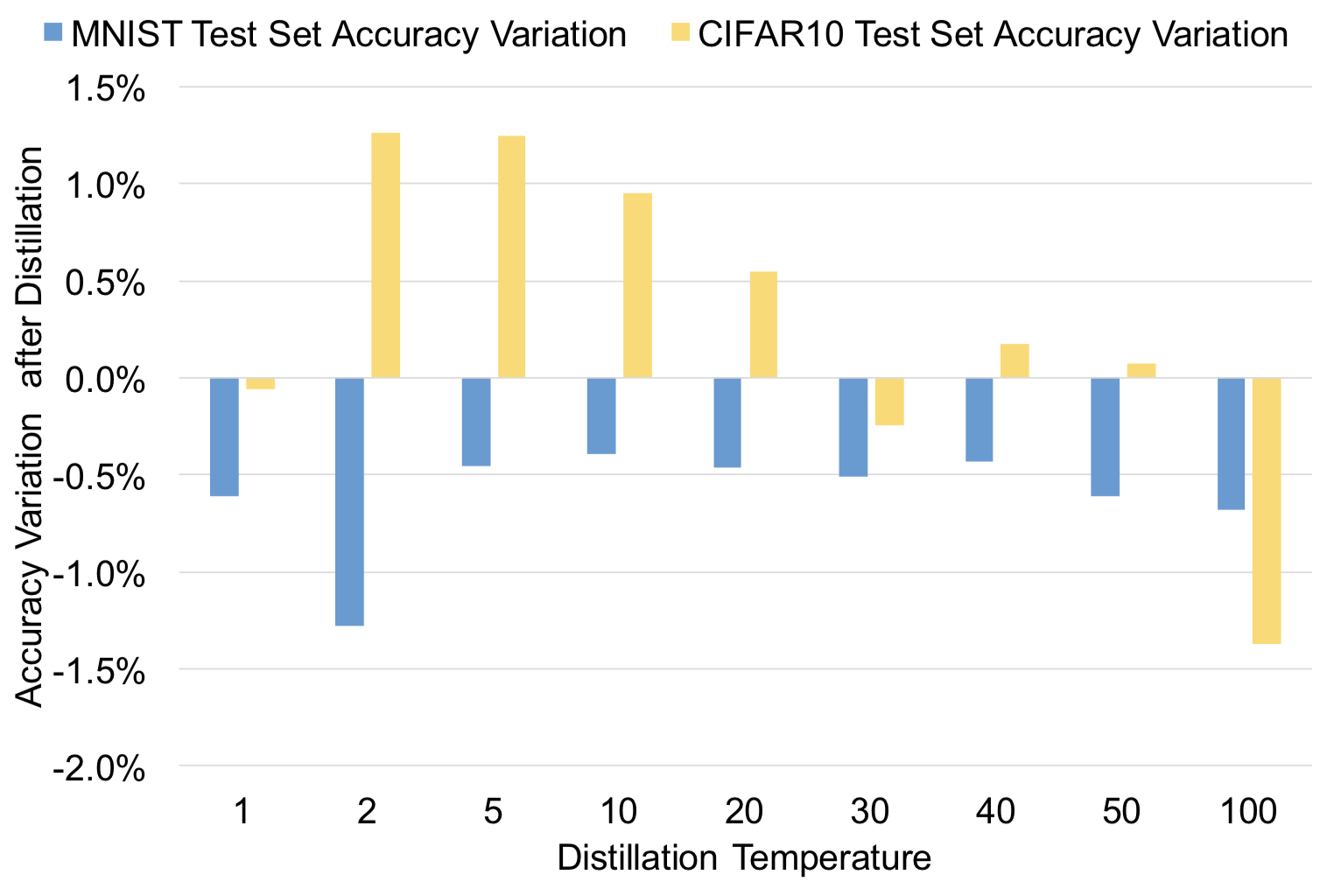
Source: Papernot et al. (2015a)


Distillationである程度攻撃を防げそうなことは分かりました。しかし、そもそもなぜ攻撃を防げるようになるのでしょうか。理由の一つは勾配にありそうです。微分を計算してみると、

となっています。 \(T\) が大きくなると勾配は小さくなっていきそうです。勾配が小さいということは、入力により大きな変化を与えなければ出力を変化させることができないことになります。あまりにも大きな摂動を与えると、人間が変化に気づけるようになってしまうため攻撃がより難しくなります。

（テスト時は\(T=1\)としているので実際にはもう少し複雑なのですが、論文の実験結果をみてもちゃんと \(T\) が大きくなるほど、勾配が小さくなっています。）

他にもdistillationで防御できる理由として、regularizerとしての効果でoverfittingを防げるということがあるかもしれません。しかし、Goodfellow et al. (2014)の議論ではadversarial exampleはoverfittingによるものではないということだったので、これが本当に理由なのかは疑問が残るところです。

残念ながらdefensive distillationも完璧な防御方法ではなく、distillationしたモデルも攻撃できたという報告があります（Carlini and Wagner 2016）。また、オリジナルのdefensive distillationを拡張したモデルも出てきています（Papernot and McDaniel 2017）。


Gradient Masking

これまで見てきたように、ほとんどの攻撃手法は勾配を利用しています。勾配を利用しているのであれば、何らかの方法で勾配を利用できないようにすることで攻撃を防ぐことができないでしょうか。

機械学習のAPIについて考えると、猫である確率が98.37857%のように確率が得られる場合がよくあります。確率が得られると、どのように画像を変化させるとその確率が下がるのかという手がかりが得られます。その方向にもっと画像を変化させれば、別のクラスに誤分類させてしまうことができるはずです。

このAPIが確率を返さず、「猫」のようなラベルだけを返すようにしてはどうでしょうか。画像を僅かに変化させてもほとんどの場合、ラベルは猫のままでしょう。このような状況では、どの方向に画像を変化させれば誤分類させることができるのか手がかりがありません。

また、下図(a)のように、入力に対する勾配がほとんどゼロになるようにそもそもモデルに学習させるという方法も考えられます。


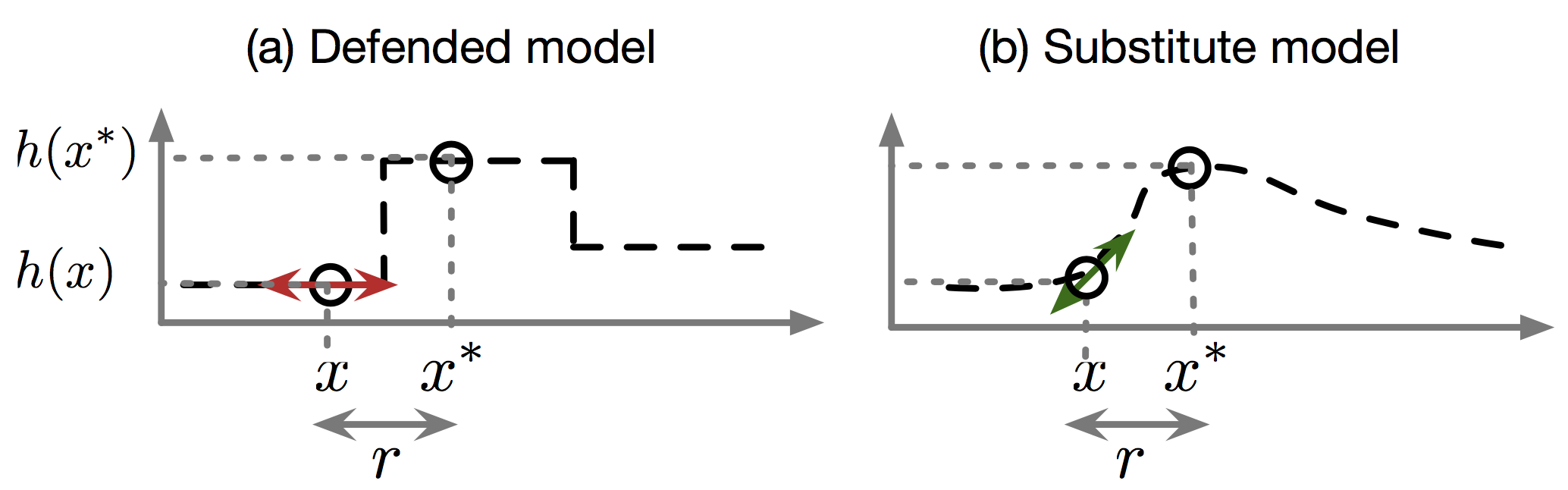
Source: Papernot et al. (2016c)


このようにgradient maskingで完璧に防御できるかというと残念ながらそうではありません。Black-box attackのところで見たように、手元で操作可能な代理のモデル（上図(b)）に学習させ、そのモデルの勾配を利用することができます。Adversarial exampleにはtransferabilityがあるため、代理のモデルで作成したadversarial exampleを使って元のモデルをだますことができてしまいます。


論文紹介


Huang et al. (2017)

これまで見てきた研究はどれも教師あり学習を想定していました。この研究では強化学習のneural network policyに対してもadversarial attackが有効であるかを検証しています。DQN、TRPO、A3Cの3つの強化学習アルゴリズムで実験していて、攻撃方法はFGSMです。

下図はPongというAtariのゲームの例です。ボールは図中の矢印の方向に動こうとしているので、paddleを下に動かせばボールをとらえることができるという状況です。元の方では”down”というactionになっていますが、攻撃を受けた方は”noop”（no-operation）になってしまっています。


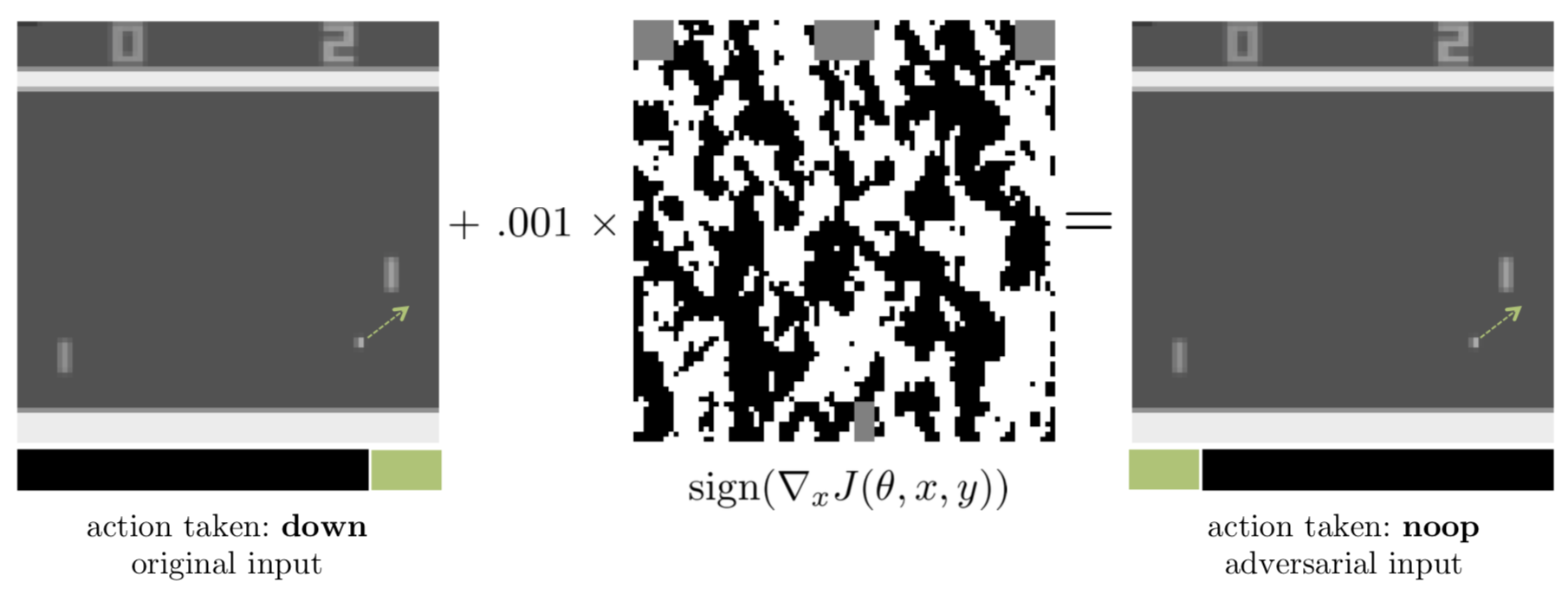
Source: Huang et al. (2017)


実験結果の動画も公開されていて、こちらはSeaquestというゲームの例です。攻撃を受けた方は明らかにスコアが落ちてしまっている様子が分かります。Adversarial exampleは強化学習でも問題になります。


Kurakin et al. (2017)

これまで見てきた例では画像を直接モデルに与えていました。しかし、防犯カメラやスマホアプリなどの例を考えると、現実問題では画像はカメラを通じて読み込まれる場合が多くあります。

このような場合でもadversarial exampleによる攻撃は有効なのでしょうか。この論文ではadversarial exampleを写真としてプリントし、それをスマホのカメラを通じて読み込ませることによって検証しています。


Source: Kurakin et al. (2017)


上図の例では、洗濯機（washer）を金庫（safe）として誤分類させることができています。 \(\epsilon\) は摂動の大きさに関する値で、ピクセルが[0, 255]の範囲で値を取る時にどれくらいの摂動を与えるかという値になっています。FGSMの場合、 \(\epsilon\) の大きさに応じて下図のように画像が変化していきます。


Source: Kurakin et al. (2017)


元々adversarial exampleとして誤分類させることができていた画像を、スマホのカメラを通じて読み込ませても必ず誤分類させられるわけではありません。この論文では3種類の方法でadversarial exampleを生成していますが、 その中ではFGSMというGoodfellow et al. (2014)で提案された手法が最もロバストであったと結論づけています。（直接画像を読み込ませる場合は他の手法の方が良かったりもします。）

論文には細かく結果が載っていますが一例を挙げると、Fast gradient sign method、\(\epsilon = 16\)、ImageNetという設定では、Top-1では約2/3、Top-5では約1/3が誤分類されることが分かっています。

また、輝度やコントラストの変化はadversarial exampleにほとんど変化を与えませんが、ぼやけ・ノイズ・JPEGの品質は影響が大きくadversarial exampleが無効化される場合があることも分かっています。adversarial exampleは非常に小さな変化を与えることで誤分類させていることを考えると自然な結果ではないでしょうか。


自動運転に関連する最近の話題

Adversarial exampleによる攻撃が懸念される最も重要な例の一つとして自動運転があります。実際の標識に埋め込み、カメラを通じて読み込んだ場合もadversarial exampleは有効でしょうか。この辺りは最近激しく議論が起きているところです。関連する論文をいくつか簡単に紹介したいと思います。

Lu et al. (2017a)は、自動運転ではadversarial exampleについて心配をする必要がないと主張しています。プリントしても有効なadversarial exampleがあることは分かっていますが、これらの実験ではカメラの距離や角度はほとんど同じになっています。著者らはadversarial exampleはスケールに対して敏感で、カメラの距離や角度が変わると有効ではなくなると指摘しています。自動運転車は移動するのでadversarial exampleのスケールが変化し、ほとんどの場合で正しく分類できることになります。

Athalye and Sutskever (2017)はスケールや角度が変わっても有効なadversarial exampleを生成できることを示しています。これについてはOpenAI Blogでも紹介されています。


Source: OpenAI Blog


Evtimov et al. (2017)もロバストな攻撃方法を提案しています。下の動画の左側は攻撃を受けた標識です。”Stop”という標識であるにも関わらず、”Speed Limit 45”の標識として認識されてしまっています。



これに対してLu et al. (2017b)がさらに反論しています。Evtimov et al. (2017)では、標識をクロップ・リサイズしたものを標識分類器に流し込んでいました。このプロセスを経ることによって、スケールの違いなどの影響がなくなってしまうと考えられます。単純な分類器ではなく、物体検出によく使われるYOLOやFaster R-CNNといったモデルはだまされることなく”Stop”の標識を認識することができたと報告されています。

この辺りの議論は今後も続いていきそうです。


まとめ


そもそもadversarial exampleとは何なのかというところから始まり、様々な攻撃・防御手法や事例を紹介してきました。今後この記事を更新する形で追加で論文紹介していくかもしれません。この記事がadversarial exampleの理解や動向を追うのに少しでも役立てば嬉しいです。


参考文献