Kerasの公式ブログにAutoencoder（自己符号化器）に関する記事があります。今回はこの記事の流れに沿って実装しつつ、Autoencoderの解説をしていきたいと思います。間違いがあれば指摘して下さい。また、Kerasの公式ブログはKerasでの実装に関してだけでなく、機械学習自体についても勉強になることが多く、非常におすすめです。

今回の記事では様々なタイプのAutoencoderを紹介しますが、日本語ではあまり聞き慣れないものもあるかと思いますので、今回は名称を英語で統一したいと思います。

目次


イントロダクション

Autoencoderはこれから見ていくように様々な種類のものがあるのですが、基本的には下図のように、入力と出力が同じになるようにニューラルネットワークを学習させるものです。入力をラベルとして扱っていて、教師あり学習と教師なし学習の中間に位置するような存在です。普通のニューラルネットワークと同様に勾配降下法（gradient descent）などを使って学習させることができます。

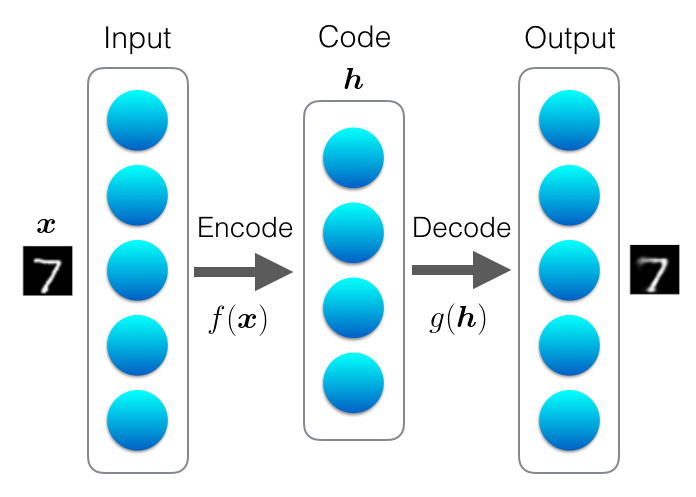
Autoencoderの概念図

人間も何かを覚える時には、見たものを頭の中で再現してみたりしますが、それと似ているところも面白いです。人間がやっていることを導入することでうまくいくようになるというのが、ニューラルネットワークの面白さの一つではないでしょうか。

僕は元々物理出身なのですが、物理学者リチャード・ファインマンの有名な名言に、

“What I cannot create, I do not understand.”
「作ってみせることができなければ、理解したとはいえない」

というものがあります。Autoencoderには、これに通じるものも感じます。

Autoencoderはこれまで次元削減や表現学習（feature learning）などの用途で使われてきましたが、表現学習を目的として使われることは少なくなってきています。深いニューラルネットワークでもランダムに初期化した状態からうまく学習できるようになったためです。

最近では、生成モデル（generative model）としての利用も注目されています。生成モデルについては別記事を書く予定です。

それでは、それぞれのモデルについて見ていきましょう。


Undercomplete Autoencoder

Autoencoderでは通常はその出力ではなく、うまく特徴を抽出することの方に興味があります。どのようにすれば意味のある特徴を抽出できるでしょうか。

まず、エンコードされたデータ（コードと呼ばれる）の次元数（Autoencoderの概念図の中央部分の丸の数）について考えてみます。この次元数が入力と同じ、またはそれよりも大きい場合はどうなるでしょうか。この場合、入力の値を単純にコピーすることにより、出力層にて入力を再現できてしまいます。入力を完璧に再現することができますが、単純に値をコピーしているだけであり、何か役立つ特徴を抽出しているわけではありません。

単純なコピーではない特徴を抽出する手法は様々なものが提案されていますが、一番単純なものはコードの次元数を入力の次元数よりも小さくしてしまうというものです。単純に値をコピーするだけではうまく入力を再現することができず、重要な特徴を抽出することが強制されます。このように、コードの次元が入力の次元よりも小さくなるようなものをUndercomplete Autoencoderと呼びます。

活性化関数が恒等写像（つまり活性化関数なし）で、損失関数が二乗誤差の場合は、主成分分析（principal component analysis, PCA）に相当することが知られています。Autoencoderでは活性化関数を非線形にすることができるので、Autoencoderは非線形の主成分分析を行っていると考えることができます。

一方、入力よりもエンコード後の次元数の方が大きいものはOvercomplete Autoencoderと呼ばれます。こちらはそのままでは役に立ちませんが、損失関数を変更することにより制約を加えてやったり、ノイズを加えてやったりすることにより意味のある特徴を抽出できるようになります。これらはRegularized Autoencoderと呼ばれます。

それでは、シンプルな構成のUndercomplete Autoencoderを実装してみましょう。データセットはMNISTを使用します。MNISTは28x28のグレースケールの画像で構成されており、訓練データ(training set)が60,000枚、テストデータ(test set)が10,000枚となっています。小さなデータセットですので、CPUで十分計算することができます。

from keras.layers import Input, Dense
from keras.models import Model
from keras.datasets import mnist
import numpy as np

encoding_dim = 32
input_img = Input(shape=(784,))
encoded = Dense(encoding_dim, activation='relu')(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input=input_img, output=decoded)

autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

入力と出力は784次元で、中間層は32次元になっています。エンコーダとデコーダで重みを共有する場合がありますが、ここではそれぞれ別の重みを使用しています。

Modelを使うよりも、Sequentialに慣れている人が多いかと思いますが、encodedのような変数を後から利用できるように、今回はこのような実装方法で進めていきます。Sequentialで実装することも可能です。

オプティマイザにはAdadelta、損失関数にはバイナリエントロピー（binary cross-entropy）を使用しています。下記のように画像データは0から1の値を取るように規格化していて、出力も0から1になるように出力層の活性化関数にはシグモイドを適用しています。

次にデータを読み込み、学習させます。

from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

autoencoder.fit(x_train, x_train,
                nb_epoch=50,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

MNISTのデータを読み込んだ後、配列を変形しています。x_trainは (60000, 28, 28) という形をしていますが、784次元の入力になるように (60000, 784) に変形しています。また、Autoencoderなので、入力画像がラベルとしても使われます。

50エポック計算すると、訓練誤差やテスト誤差は共に0.10程度になります。

学習した重みを保存したり、読み込みたい場合は以下のようにすることができます。

autoencoder.save_weights('autoencoder.h5')
autoencoder.load_weights('autoencoder.h5')

次に、入力画像と出力画像を可視化してみます。

import matplotlib.pyplot as plt

# テスト画像を変換
decoded_imgs = autoencoder.predict(x_test)

# 何個表示するか
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
    # オリジナルのテスト画像を表示
    ax = plt.subplot(2, n, i+1)
    plt.imshow(x_test[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

    # 変換された画像を表示
    ax = plt.subplot(2, n, i+1+n)
    plt.imshow(decoded_imgs[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

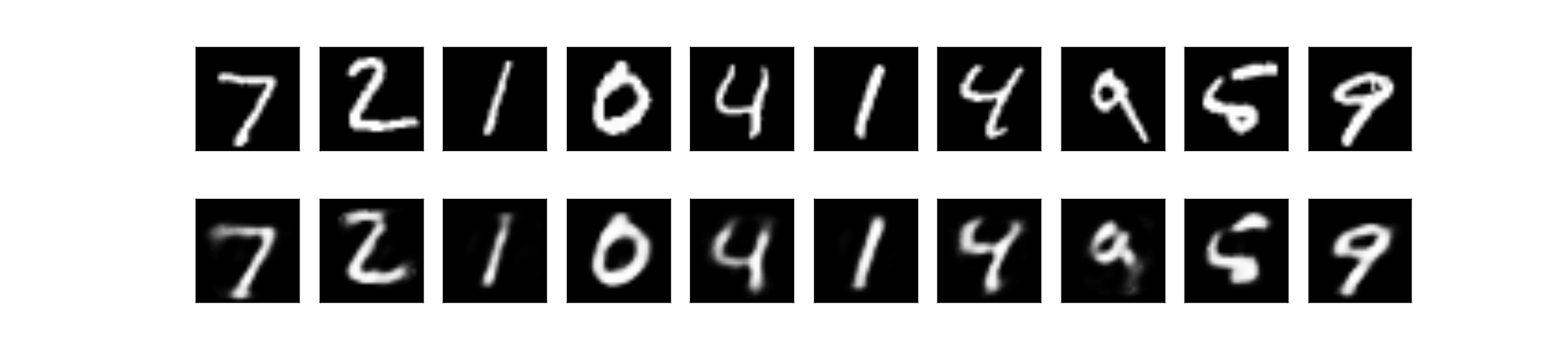
上段：オリジナル画像　下段：出力画像

無事に可視化することができました。オリジナルに近い画像を出力できていることが分かります。

オプティマイザはAdadeltaを使用しましたが、最近よく使われるAdamにするとどうでしょうか。結果はこのようになります。

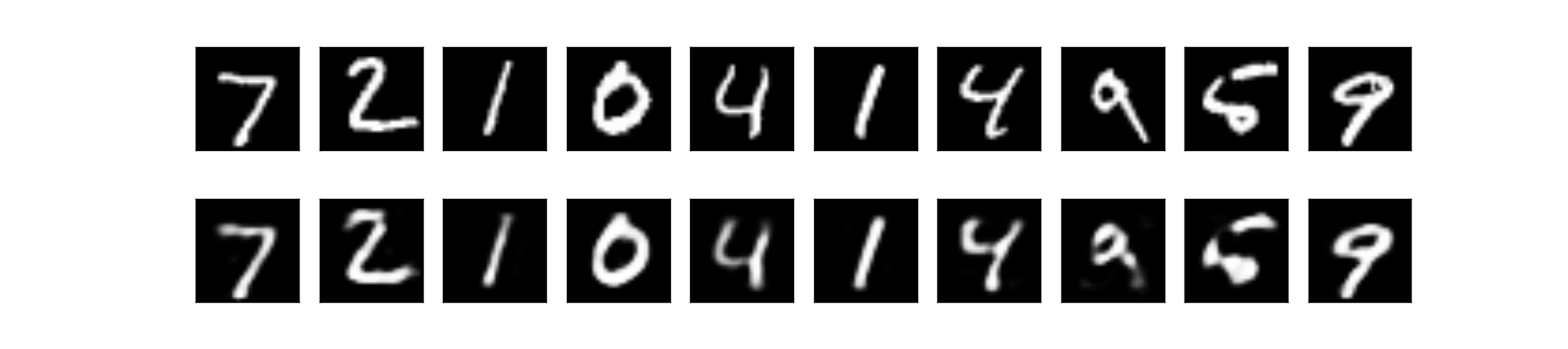
上段：オリジナル画像　下段：出力画像

Adadeltaの場合と見た目はほとんど変わりませんが、訓練誤差とテスト誤差の値は少し小さくなって0.092程度になりました。以下ではAdamを使用していきたいと思います。オプティマイザについては過去記事でも簡単に紹介しています。オプティマイザについてより詳しくまとめた記事もそのうち書いてみたいと思っています。


Sparse Autoencoder

入力を\(\boldsymbol{x} \)、エンコードされたものを\(\boldsymbol{h} = f(\boldsymbol{x}) \)とすると（\(\boldsymbol{h}\)はコードと呼ばれます）、Sparse Autoencoderの損失関数は次のように表されます。

ここで、\(g\)はデコード、\(\Omega(\boldsymbol{h})\)はペナルティを表します。

入力よりもコードの次元が多いOvercomplete Autoencoderでも、このペナルティの存在により、単純に値をコピーするのではなく、うまく特徴を学習できるようになります。

このペナルティは重み減衰（weight decay）のような正則化（regularization）と似ているように見えますが、それとは異なることに注意する必要があります。重み\(W\)ではなく、コード\(\boldsymbol{h}\)に対する制約になっています。

このペナルティの存在によって、中間層で活性化するニューロンがより少なくなり疎になります。人間で考えても、ほとんどのニューロンが発火してしまうよりも、少ないニューロンの発火で再現できる方がエネルギー効率の面でも良いはずで、メリットがあるでしょう。

では、実装してみましょう。

from keras import regularizers

encoding_dim = 32
input_img = Input(shape=(784,))

# activity regularizerを加える
encoded = Dense(encoding_dim, activation='relu',
                activity_regularizer=regularizers.activity_l1(1e-4))(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input=input_img, output=decoded)

autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder.fit(x_train, x_train,
                nb_epoch=100,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

regularizers.activity_l1()の部分がペナルティ項に対応しています。これは\( \Omega (\boldsymbol{h}) = \lambda \sum |h_i| \)に相当します。得られた画像は以下です。

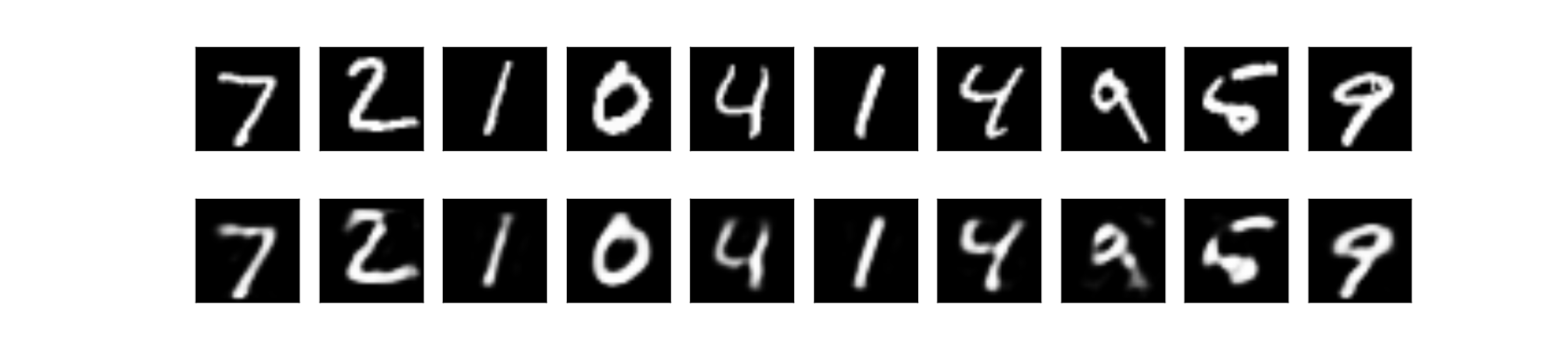
上段：オリジナル画像　下段：出力画像

訓練誤差が約0.097、テスト誤差が約0.092という結果が得られました。出力画像の見た目も、テスト誤差も、どちらもペナルティがない時とほとんど変わらないように見えます。

中間層の平均活性度を見てみましょう。ペナルティ\( \Omega (\boldsymbol{h}) \)によって平均活性度が小さくなっていると考えられます。以下のようにして確認することができます。

encoder = Model(input=input_img, output=encoded)
encoded_imgs = encoder.predict(x_test)

print('encoded img mean:', encoded_imgs.mean())
# ('encoded img mean:', 1.2807794804895529)

1.28という値が得られました。ペナルティ項がない場合は、8.86という値になります。ペナルティを加えることにより、中間層における平均活性度が小さくなっていることが分かります。


Deep Autoencoder

ここでは中間層の数を増やし、深くすることを考えます。これによってどんなメリットがあるでしょうか。

これまで見てきたように、Autoencoderは順伝播型ニューラルネットワーク（feedforward neural network）です。そのため、Autoencoderも順伝播型ニューラルネットワークで層を増やした場合のメリットを享受できると考えられます。ちなみに順伝播型ニューラルネットワークは再帰的ニューラルネットワークのようにループしたりしないもののことです。

Universal approximation theoremという定理があり、順伝播型ニューラルネットワークの場合、中間層が1層以上、かつ中間層おけるニューロン数が十分大きければ、基本的にどんな関数でも近似できることが保証されています（厳密にはもう少し細かい条件がありますが）。これまで見てきたAutoencoderでエンコーダの部分だけを考えると中間層が存在していません。そこに一つ以上の中間層を加えることにより、エンコーダの表現力が増すと考えることができます。

では中間層が1層あれば、どんな関数でも学習できるようになったと考えてよいのでしょうか。実はそうではありません。十分な表現力があるからといって、「学習」できるかどうかは別問題だからです。

アルゴリズム上の問題でうまく学習できない可能性があります。そのアルゴリズムでは最適なパラメータになるまで学習を進めることができないかもしれません。原理的にはかなり近い関数を学習可能だとしても、必要となる中間層のニューロン数が膨大で計算時間がかかり過ぎてしまう可能性が考えられます。また、そもそも違う関数に向かって学習が進んでしまう可能性も考えられます。

しかし、様々な研究により、層を増やして深くすることで、計算コストが小さくなったり、少ないデータで学習できるようになったり、正確度が上がったりする場合があることが示されています。

それでは、深くしたモデルを実際に実装してみましょう。

encoding_dim = 32
input_img = Input(shape=(784,))

encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(64, activation='relu')(encoded)
encoded = Dense(32, activation='relu')(encoded)

decoded = Dense(64, activation='relu')(encoded)
decoded = Dense(128, activation='relu')(decoded)
decoded = Dense(784, activation='sigmoid')(decoded)

autoencoder = Model(input=input_img, output=decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder.fit(x_train, x_train,
                nb_epoch=100,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

得られた画像は以下です。

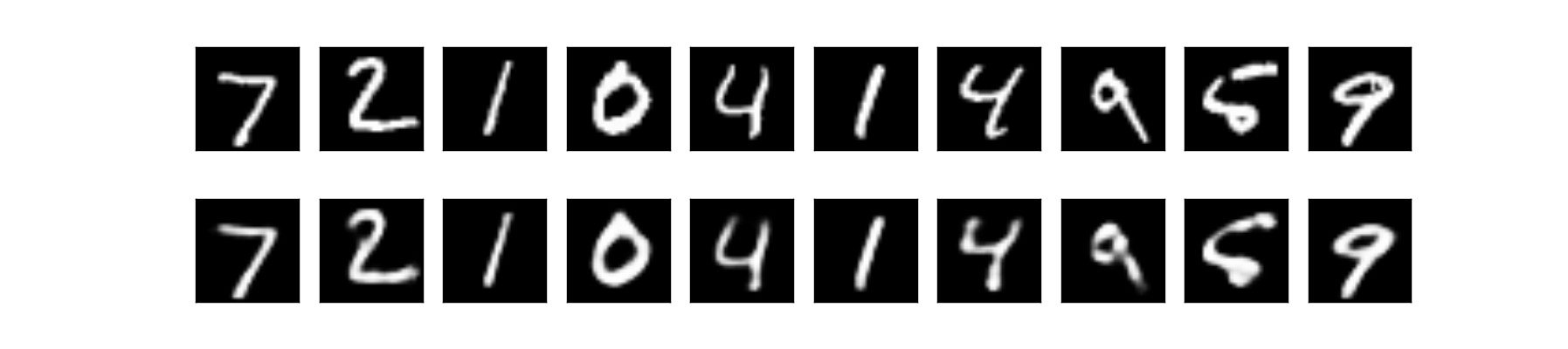
上段：オリジナル画像　下段：出力画像

訓練誤差・テスト誤差は共に約0.082となりました。中間層が1層の場合は約0.092だったので、誤差が小さくなっていることが分かります。


Convolutional Autoencoder

今度は畳み込みニューラルネットワーク（convolutional neural network, CNN）を使うことを考えます。

一般に、主に画像認識においてCNNは普通のニューラルネットワーク（multilayer perceptron, MLP）よりもパフォーマンスが高いことが知られています。AutoencoderでもCNNを使うことにより、うまく学習できることが期待されます。ここで研究を一つ紹介します（Autoencoderではなく普通のCNN・MLPに関する研究です）。

Urban et al. 2016では、深さや畳み込みが本当に重要かどうかを実験により検証しています。この研究では、蒸留（distillation）という手法を使って学習させています。本題からどんどんそれていく気もしますが、面白い手法ですので蒸留について簡単に説明します。

蒸留では教師モデルと生徒モデルを用意します。通常は訓練データのラベルを使って学習しますが、蒸留ではこのラベルではなく、教師モデルによる予測をラベルとして生徒モデルを学習させます。生徒モデルは、教師モデルの予測と生徒モデルの予測が最小となるように学習していきます（ラベルも両方使う場合があります。参考：Hinton et al. 2015）。

通常のラベルを使った学習では、例えば猫に関する訓練データであれば、猫以外のクラスに属する確率はゼロとして扱われます。しかし、教師モデルの予測では、猫である確率が一番高くとも、犬や虎である確率も僅かに存在しているはずです。生徒モデルは、ラベルとは異なる他のクラスである確率も含めて学習することになります。

蒸留を行うと、生徒モデルは教師モデルよりも浅く小さなモデルであるにも関わらず、教師モデルと同等の正確度を出せることが分かっています。教師モデルの予測は、正解となるクラスだけでなく、それ以外のクラスに対する確率も含んでいるため、より多くの情報を持っていることになります。これにより、生徒モデルはうまく学習できると考えられます。

生徒モデルは教師モデルよりも小さなモデルであるため、少ない計算量で済むようになります。何かサービスをリリースする時には蒸留を使って、生徒モデルをデプロイすると良さそうです。

Deep Autoencoderの章で、中間層が1層以上あれば十分な表現力を持てるがうまく学習できるかどうかは別問題という話をしました。今のところ、浅いニューラルネットワークに学習させる最も良い方法は蒸留だと考えられます。蒸留によって限界性能を引き出しつつ、層数や畳み込みによってどう正確度が変化するかを見れば、層数や畳み込みの重要性をある程度見極めることができるでしょう。では実験結果を見てみましょう。

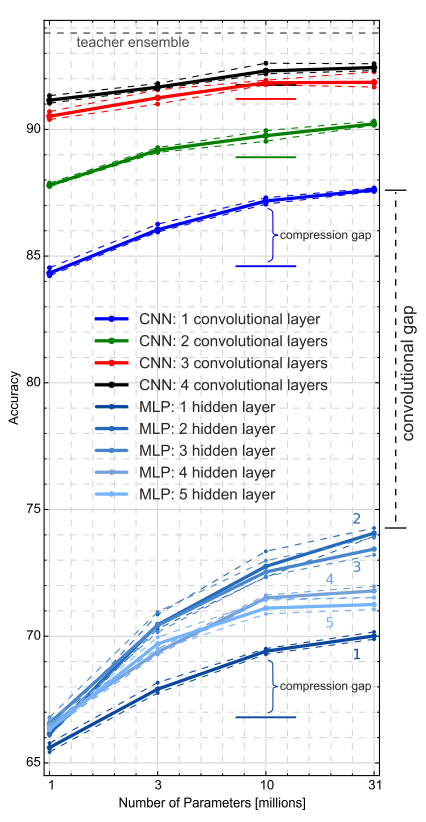
生徒モデルの精度の変化。データはCIFAR10を使用。10Mに位置する水平方向の線は、蒸留なしで学習させた場合の正確度を示す。Urban et al. 2016より引用

横軸はパラメータ数になっており、パラメータ数を同じにした条件で比較することができます。まず、畳み込み層の存在は非常に重要であることが分かります。さらにCNN同士で比較すると深さも非常に重要であることが分かります。パラメータ数を増やすことによっても正確度は上がりますが、深さごとに限界があるように見えます。

MLPの結果を見ると、深いほどいいというわけではなく、4・5層よりも2・3層の方が良いという点も面白いです。

この研究結果は普通のCNN・MLPに対するものですが、Autoencoderでも畳み込み層を入れることにより、うまく学習できるようになることが期待されます。では実装してみましょう。

from keras.layers import Input, Convolution2D, MaxPooling2D, UpSampling2D
from keras.models import Model

input_img = Input(shape=(1, 28, 28))

x = Convolution2D(16, 3, 3, activation='relu', border_mode='same')(input_img)
x = MaxPooling2D((2, 2), border_mode='same')(x)
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(x)
x = MaxPooling2D((2, 2), border_mode='same')(x)
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(x)
encoded = MaxPooling2D((2, 2), border_mode='same')(x)

x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(x)
x = UpSampling2D((2, 2))(x)
x = Convolution2D(16, 3, 3, activation='relu')(x)
x = UpSampling2D((2, 2))(x)
decoded = Convolution2D(1, 3, 3, activation='sigmoid', border_mode='same')(x)

autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

まずは畳み込み層を見てみましょう。デフォルトではborder_mode='valid'なのですが、’same’を指定しています。’valid’の場合、（フィルタのサイズやストライドにもよりますが）出力のサイズは入力に対して小さくなります。一方、’same’を指定するとゼロパディングが適用され、畳み込み層の入力と出力のサイズが同じになります（ストライドが1の場合）。

プーリング層では、pool_size=(2, 2)と設定しています。ストライドを指定しない場合は、pool_sizeと同じ幅のストライドが適用されます。

エンコードの過程でプーリングを行っている（downsampling）のでサイズが小さくなっています。デコード時にはこのサイズを大きくしてやる必要があるのでUpSampling2Dを使っています。UpSampling2D((2, 2))の場合は、1つの入力に対して同じ値が4つ出力されることになります。

途中の入力や出力の形がどうなっているのかイメージしづらいと思いますので、図を出力してみましょう。

from keras.utils.visualize_util import plot
plot(autoencoder, to_file="architecture.png", show_shapes=True)

とするだけで簡単に出力することができます。



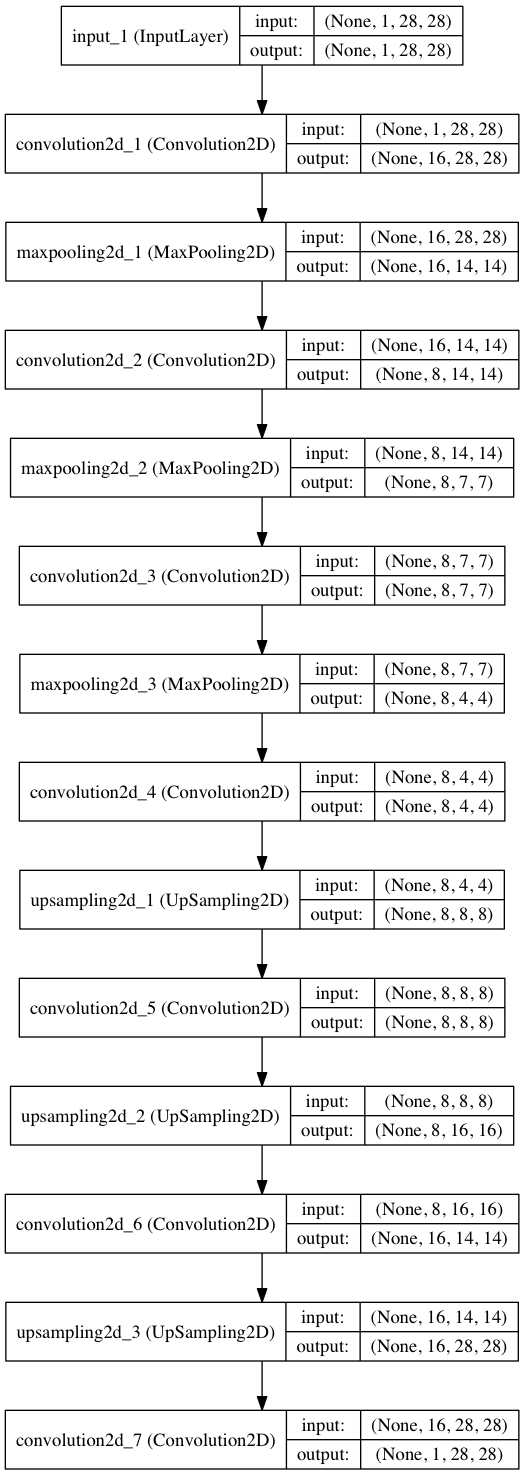
真ん中では (8, 4, 4) という形になっていますが、出力では (1, 28, 28) と入力と同じ形に戻っていることが分かります。

次に、訓練データとテストデータを読み込みます。

from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 1, 28, 28))
x_test = np.reshape(x_test, (len(x_test), 1, 28, 28))

mnist.load_data()で読み込んだ直後のx_trainは (60000, 28, 28) という形をしていますが、これを畳み込みニューラルネットワーク（convolutional neural network, CNN）でよく使われる形 (60000, 1, 28, 28) に変換しています。MNISTはグレースケールの画像なのでチャネルが1となっています。x_testも同様の変換を行っています。

今回はTensorBoardを使って学習曲線を出力してみましょう。KerasのバックエンドはTensorFlowまたはTheanoから選択することができますが、TensorBoardを使うためにはTensorFlowに設定しておく必要があります。バックエンドは~/.keras/keras.jsonという設定ファイルで切り替えることができます。

{
    "image_dim_ordering": "th",
    "epsilon": 1e-07,
    "floatx": "float32",
    "backend": "tensorflow"
}

次にターミナルでTensorBoardサーバーを立ち上げ、/tmp/autoencoderに保存してあるログを読み込むようにします。

$ tensorboard --logdir=/tmp/autoencoder

autoencoder.fit(x_train, x_train,
                       nb_epoch=50,
                       batch_size=128,
                       shuffle=True,
                       validation_data=(x_test, x_test),
                       callbacks=[TensorBoard(log_dir='/tmp/autoencoder')])

http://0.0.0.0:6006（逆さまにするとgoog(le)になる）にブラウザからアクセスすると、学習の経過をリアルタイムでモニタリングすることができます。

CPUで試したところ1エポックあたり350秒程度かかりました。CPUでもギリギリいける範囲かもしれませんが、GPUが使えるのであればそちらの方が良いかと思います。AWSのGPUでは1エポックあたり50秒程度でした。

TensorFlowの場合は、GPUを利用できる環境で実行すると、CPUの場合と同じように実行するだけで自動的にGPUを使って計算してくれます。TheanoでのGPUの使用方法は過去記事で紹介していますので、そちらも参考にしてみてください。

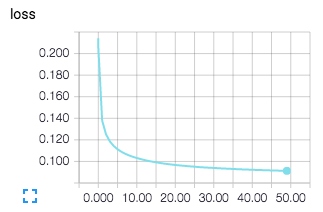
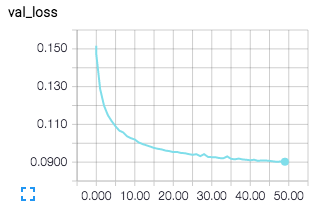
左図：訓練誤差　右図：テスト誤差

今回は50エポックまで計算しましたが、計算を続ければまだまだ誤差が小さくなりそうです。

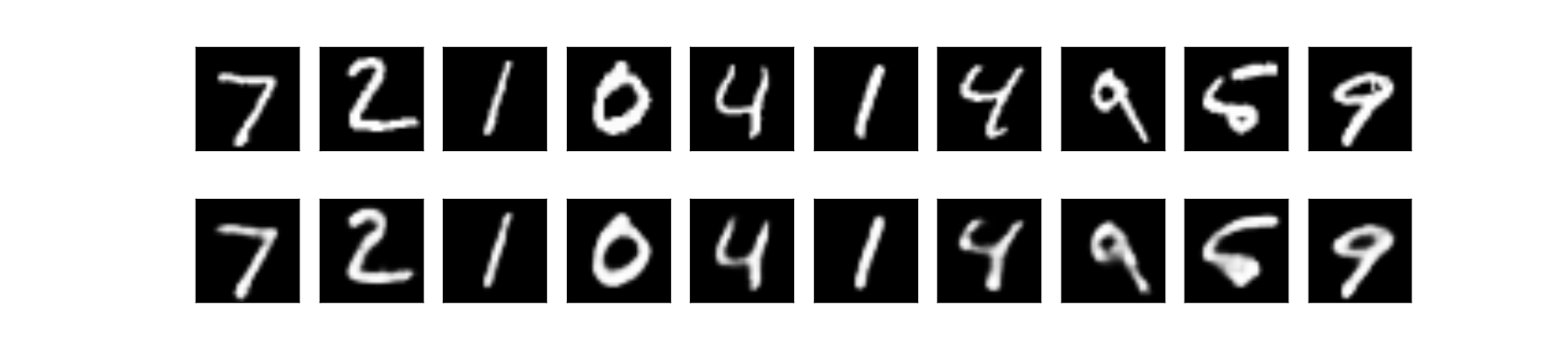
上段：オリジナル画像　下段：出力画像

せっかくなので、エンコードされた画像も可視化してみましょう。(8, 4, 4) という形をしています。以下のようにして出力することができます。

import matplotlib.pyplot as plt

n = 10
encoder = Model(input_img, encoded)
encoded_imgs = encoder.predict(x_test[:n])

plt.figure(figsize=(20, 8))
for i in range(n):
    for j in range(8):
        ax = plt.subplot(8, n, j*n + i+1)
        plt.imshow(encoded_imgs[i][j], interpolation='none')
        plt.gray()
        ax.get_xaxis().set_visible(False)
        ax.get_yaxis().set_visible(False)
plt.show()

エンコードされた画像

エンコードされた画像は、このように人間には認識できない画像になっています。また、Matplotlibはデフォルトでは補完して出力するようになっていますが、4x4の解像度が低い画像は生の値で出力した方が良いと思うので、interpolation='none'と指定しています。Matplotlibの補完に関してはこちらの記事が参考になるかと思います。


Denoising Autoencoder

Autoencoderでは、基本的に損失関数が

という形をしていて、単純に入力と出力の違いがなるべく小さくなるように学習していくのでした。そして、Overcomplete Autoencoderというコード\(\boldsymbol{h}\)の次元が入力\(\boldsymbol{x}\)の次元よりも大きいモデルでは、単純に値をコピーすることで、入力と出力の違いをゼロにできてしまうという問題がありました。

この問題を解決するために、Sparse Autoencoderでは\(\Omega(\boldsymbol{h})\)というペナルティ項を入れました。ここでは別のアプローチを考えます。

Denoising Autoencoder (DAE)では、

を最小化します。ここで、\(\tilde{\boldsymbol{x}}\)は入力にノイズを加えたものを表します。ノイズが加わった入力からオリジナルの入力を復元しないといけないので、単純に値をコピーするわけにはいかなくなります。そのため、ノイズを除去するだけでなく、良い特徴を学習できるようになると考えられます。

また、別の考え方として下図のような見方をすることもできます。

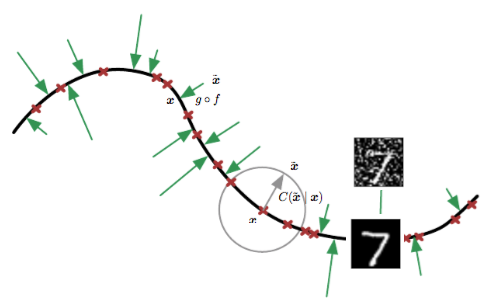
Goodfellow et al. 2016 Bookの図をもとに作成

黒い線は、低次元に折りたたまれた\(\boldsymbol{x}\)の分布を表します。赤い印は、それぞれの訓練データに対応します。これらの訓練データにノイズを加える操作は、灰色の線のように、\(\boldsymbol{x}\)の分布から少し外れた場所を考えることを意味します。緑の矢印は、ノイズが加わったデータ\(\tilde{\boldsymbol{x}}\)を\(\boldsymbol{x}\)にマッピングする様子を表しています。Denoising Autoencoderは、\(\tilde{\boldsymbol{x}}\)から\(\boldsymbol{x}\)をうまく復元できるように学習していくため、この緑の矢印を学習していると考えることもできるでしょう。

では実装してみましょう。まず、正規分布のノイズを加え、0から1の間の値を取るようにクリップします。

from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 1, 28, 28))
x_test = np.reshape(x_test, (len(x_test), 1, 28, 28))

noise_factor = 0.5
# 平均0、標準偏差1の正規分布
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0., scale=1., size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0., scale=1., size=x_test.shape)

x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)

画像を出力することにより、ノイズが加わっているかどうか確認してみましょう。

import matplotlib.pyplot as plt

n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
    ax = plt.subplot(1, n, i+1)
    plt.imshow(x_test_noisy[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

ノイズを加えた画像

無事にノイズを加えることができました。なんとか元の文字を認識することができますが、認識がかなり困難なものもあります。Autoencoderはうまくノイズを除去することができるでしょうか。Convolutional Autoencoderの章で扱ったモデルを少し変更し、フィルタを多くしてみます。

from keras.layers import Input, Convolution2D, MaxPooling2D, UpSampling2D
from keras.models import Model

input_img = Input(shape=(1, 28, 28))
x = Convolution2D(32, 3, 3, activation='relu', border_mode='same')(input_img)
x = MaxPooling2D((2, 2), border_mode='same')(x)
x = Convolution2D(32, 3, 3, activation='relu', border_mode='same')(x)
encoded = MaxPooling2D((2, 2), border_mode='same')(x)

x = Convolution2D(32, 3, 3, activation='relu', border_mode='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Convolution2D(32, 3, 3, activation='relu', border_mode='same')(x)
x = UpSampling2D((2, 2))(x)
decoded = Convolution2D(1, 3, 3, activation='sigmoid', border_mode='same')(x)

autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

各層の入出力が分かりやすいように、ここでも図を載せておきます。



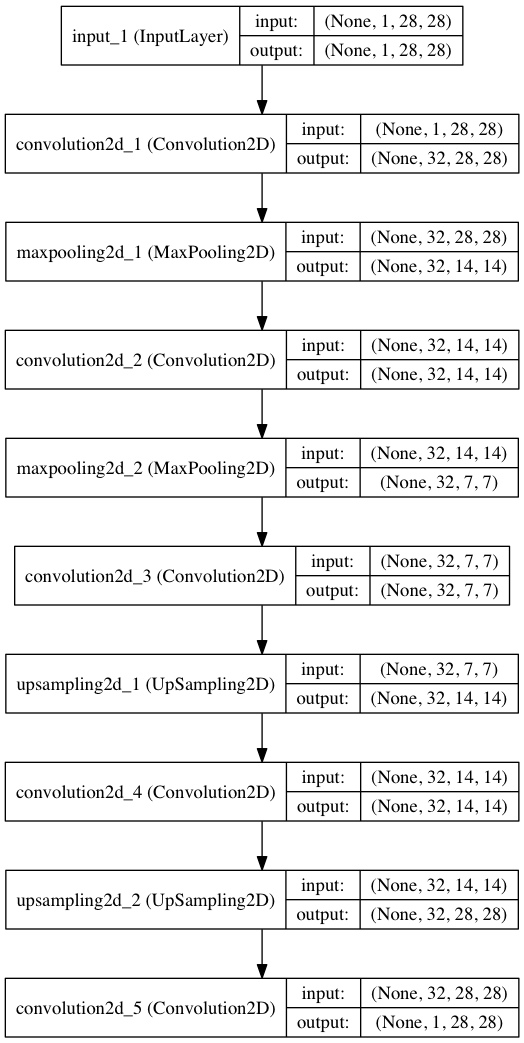
ノイズを加えた画像を入力、ノイズのないオリジナルの画像をラベルとして学習させます。

autoencoder.fit(x_train_noisy, x_train,
                nb_epoch=100,
                batch_size=128,
                shuffle=True,
                validation_data=(x_test_noisy, x_test),
                callbacks=[TensorBoard(write_graph=False)])

TensorBoardはデフォルトではlog_dir='./logs'という設定になり、./logs配下にログが出力されます。ディレクトリが存在しない場合は自動的に作られます。また、write_graph=Falseと指定することにより、グラフを出力しないようになり、ログファイルのサイズが小さくなります。デフォルトではTrueに設定されています。

CPUだと1エポックあたり約750秒もかかってしまうので、GPUを使うと良いと思います。GPUの場合は1エポックあたり100秒程度です。

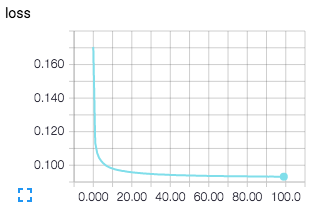
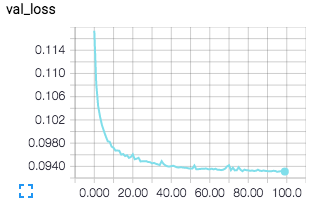
左図：訓練誤差　右図：テスト誤差

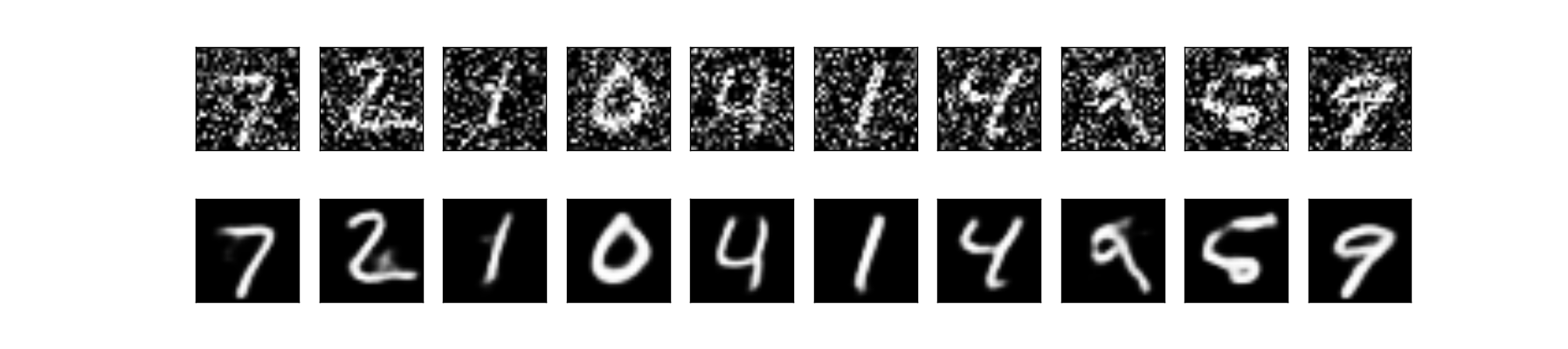
上段：ノイズを加えた画像　下段：出力画像

無事にノイズを除去することができました。ノイズを加えた画像は人間が見ても認識が困難になっているものもありますが、かなりうまくノイズを除去できていることが分かります。


まとめ

中間層が1層の単純なAutoencoderから始まり、簡単な解説を加えながらDenoising Autoencoderなど様々なAutoencoderを見ていきました。Kerasを使って非常に簡単に実装することもできました。

他に有名なものとしては、生成モデルの一つであるVariational Autoencoder (VAE)があります。別記事としてこちらも紹介したいと思っています。


参考文献